
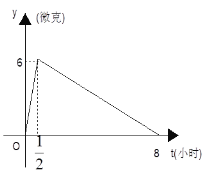
【题目】某医药研究所开发一种新药,如果成人按规定的剂量服用,据监测:服药后每毫升血液中含药量y与时间t之间近似满足如图所示曲线:
(1)分别求出![]() 和
和![]() 时,y与t之间的函数关系式;
时,y与t之间的函数关系式;
(2)据测定:每毫升血液中含药量不少于4微克时治疗疾病有效,假如某病人一天中第一次服药为7:00,那么服药后几点到几点有效?
【答案】(1) 当![]() 时,y1=12t; 当t≥
时,y1=12t; 当t≥![]() 时,
时,![]() ;(2) 7:20到10:00有效.
;(2) 7:20到10:00有效.
【解析】
(1)当![]() 时,y与t成正比例函数,
时,y与t成正比例函数,![]() 时,y与t是一次函数关系,利用待定系数法求解即可.
时,y与t是一次函数关系,利用待定系数法求解即可.
(2)利用函数的性质把y=4分别代入两函数的解析式即可求出答案.
解:(1)当![]() 时,设y1=kt,图象经过点(
时,设y1=kt,图象经过点(![]() ,6),
,6),
代入解得:k=12,所以y1=12t.
当t≥![]() 时,设y2=kt+b,图象经过点(
时,设y2=kt+b,图象经过点(![]() ,6)和点(8,0).
,6)和点(8,0).
代入列出方程组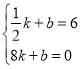
解得:![]() ,所以
,所以![]() .
.
(2)解:∵每毫升血液中含药量不少于4微克时治疗疾病有效,
∴把y=4代入y1=12t得:4=12t,
解得:t=![]() ,
,
即![]() 小时=20分钟;7点再过20分钟是7:20;
小时=20分钟;7点再过20分钟是7:20;
把y=4代入![]() 得:
得:![]() ,
,
解得:t=3,7:00再过三个小时也就是10:00.
即每毫升血液中含药量不少于4微克时是在服药后![]() 小时到3小时内有效,即从7:20到10:00有效.
小时到3小时内有效,即从7:20到10:00有效.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:初中数学 来源: 题型:
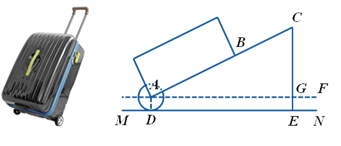
【题目】有一只拉杆式旅行箱(图1),其侧面示意图如图2所示.已知箱体长AB=50cm,拉杆![]() 的伸长距离最大时可达35cm,点A,B,C在同一条直线上.在箱体底端装有圆形的滚轮⊙A,⊙A与水平地面MN相切于点D.在拉杆伸长至最大的情况下,当点B距离水平地面38cm时,点C到水平地面的距离CE为59cm.
的伸长距离最大时可达35cm,点A,B,C在同一条直线上.在箱体底端装有圆形的滚轮⊙A,⊙A与水平地面MN相切于点D.在拉杆伸长至最大的情况下,当点B距离水平地面38cm时,点C到水平地面的距离CE为59cm.
设AF∥MN.
(1)求⊙A的半径长;
(2)当人的手自然下垂拉旅行箱时,人感到较为舒服.某人将手自然下垂在C端拉旅行箱时,CE为80cm,![]() =64°.求此时拉杆BC的伸长距离.(精确到1cm,参考数据:
=64°.求此时拉杆BC的伸长距离.(精确到1cm,参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
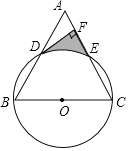
【题目】已知:如图,以等边△ABC的边BC为直径作⊙O,分别交AB,AC于点D,E,过点D作DF⊥AC交AC于点F.
(1)求证:DF是⊙O的切线;
(2)若等边△ABC的边长为8,求由![]() 、DF、EF围成的阴影部分面积.
、DF、EF围成的阴影部分面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C,D为线段AB上的两点,M,N分别是线段AC,BD的中点.
(1)如果CD=5cm,MN=8cm,求AB的长;
(2)如果AB=a,MN=b,求CD的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, BD 是△ABC 的角平分线, AE⊥ BD ,垂足为 F ,若∠ABC=35°,∠ C=50°,则∠CDE 的度数为( )

A.35°B.40°C.45°D.50°
查看答案和解析>>
科目:初中数学 来源: 题型:
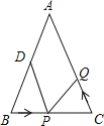
【题目】如图,已知△ABC中,∠B=∠C,BC=8cm,BD=6cm如果点P在线段BC上以1cm/s的速度由B点向C点运动,同时点Q在线段CA上由C点向A点运动,当一个点停止运动时,另一个点也随之停止运动,设点Q的速度为xcm/s,则当△BPD与△CQP全等时,x=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
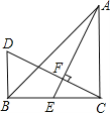
【题目】如图,△ABC中,∠ACB=90°,AC=BC,E是BC边上的一点,连接AE,过C作CF⊥AE,垂足为F,过B作BD⊥BC交CF的延长线于D.
(1)求证:△ACE≌△CBD;
(2)若BE=3![]() ,AB=6
,AB=6![]() ,求点E到AB的距离.
,求点E到AB的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,
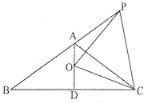
(1)求∠APO+∠DCO的度数;
(2)求证:点P在OC的垂直平分线上.
查看答案和解析>>
科目:初中数学 来源: 题型:
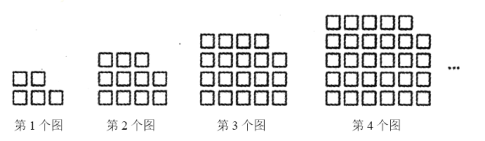
【题目】如图,用相同的小正方形按照某种规律进行摆放.根据图中小正方形的排列规律,猜想第![]() 个图中小正方形的个数为___________(用含
个图中小正方形的个数为___________(用含![]() 的式子表示)
的式子表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com