
【题目】已知:如图,以等边△ABC的边BC为直径作⊙O,分别交AB,AC于点D,E,过点D作DF⊥AC交AC于点F.
(1)求证:DF是⊙O的切线;
(2)若等边△ABC的边长为8,求由![]() 、DF、EF围成的阴影部分面积.
、DF、EF围成的阴影部分面积.
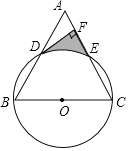
【答案】(1)证明见解析;(2)![]()
【解析】(1)连接CD、OD,先利用等腰三角形的性质证AD=BD,再证OD为△ABC的中位线得DO∥AC,根据DF⊥AC可得;
(2)连接OE、作OG⊥AC,求出EF、DF的长及∠DOE的度数,根据阴影部分面积=S梯形EFDO-S扇形DOE计算可得.
(1)如图,连接CD、OD,
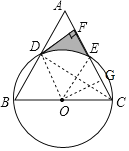
∵BC是⊙O的直径,
∴∠CDB=90°,即CD⊥AB,
又∵△ABC是等边三角形,
∴AD=BD,
∵BO=CO,
∴DO是△ABC的中位线,
∴OD∥AC,
∵DF⊥AC,
∴DF⊥OD,
∴DF是⊙O的切线;
(2)连接OE、作OG⊥AC于点G,
∴∠OGF=∠DFG=∠ODF=90°,
∴四边形OGFD是矩形,
∴FG=OD=4,
∵OC=OE=OD=OB,且∠COE=∠B=60°,
∴△OBD和△OCE均为等边三角形,
∴∠BOD=∠COE=60°,CE=OC=4,
∴EG=![]() CE=2、DF=OG=OCsin60°=2
CE=2、DF=OG=OCsin60°=2![]() ,∠DOE=60°,
,∠DOE=60°,
∴EF=FG-EG=2,
则阴影部分面积为S梯形EFDO-S扇形DOE
=![]() ×(2+4)×2
×(2+4)×2![]() -
-![]()
=![]() .
.


科目:初中数学 来源: 题型:
【题目】在□ABCD中,点E在CD上,点F在AB上,连接AE、CF、DF、BE,∠DAE=∠BCF.
(1)如图1,求证:四边形DFBE是平行四边形;
(2)如图2,若E是CD的中点,连接GH,在不添加任何辅助线的情况下,请直接写出图2中以GH为边或以GH为对角线的所有平行四边形.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E,F是平行四边形ABCD对角线AC上两点,AE=CF=![]() AC.连接DE,DF并延长,分别交AB,BC于点G,H,连接GH,则
AC.连接DE,DF并延长,分别交AB,BC于点G,H,连接GH,则![]() 的值为( )
的值为( )
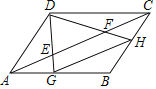
A. ![]() B.
B. ![]() C.
C. ![]() D. 1
D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,点C在∠MON的一边OM上,过点C的直线AB∥ON,CD平分∠ACM,CE⊥CD.
(1)若∠O=50°,求∠BCD的度数;
(2)求证:CE平分∠OCA;
(3)当∠O为多少度时,CA分∠OCD成1:2两部分,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年3月,我市某中学举行了“爱我中国朗诵比赛”活动,根据学生的成绩划分为A、B、C、D四个等级,并绘制了不完整的两种统计图.根据图中提供的信息,回答下列问题:
(1)参加朗诵比赛的学生共有 人,并把条形统计图补充完整;
(2)扇形统计图中,m= ,n= ;C等级对应扇形有圆心角为 度;
(3)学校欲从获A等级的学生中随机选取2人,参加市举办的朗诵比赛,请利用列表法或树形图法,求获A等级的小明参加市朗诵比赛的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系中,点![]() 的坐标是
的坐标是![]() ,点
,点![]() 是第一象限内一动点。
是第一象限内一动点。
(1) ①:如图①.若动点![]() 满足
满足![]() ,且
,且![]() ,求点
,求点![]() 的坐标。
的坐标。
②:如图②,在第(1)问的条件下,将![]() 逆时针旋转至如图
逆时针旋转至如图![]() 所示位置,求
所示位置,求![]() 的值.
的值.
(2)如图③,若点![]() 与点
与点![]() 关于轴对称,且
关于轴对称,且![]() , 若动点
, 若动点![]() 满足
满足![]() ',问:
',问:![]() 的值是否发生变化?若变化,请说明理由,若不变化,请求出其值。
的值是否发生变化?若变化,请说明理由,若不变化,请求出其值。

查看答案和解析>>
科目:初中数学 来源: 题型:
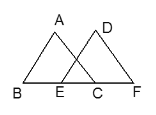
【题目】如图,已知AB∥DE,AB=DE,请你添加一个条件_______ 可以根据“ASA”使得△ABC≌△DEF;或者添加条件BE=CF,可以根据_______得到△ABC≌△DEF。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某医药研究所开发一种新药,如果成人按规定的剂量服用,据监测:服药后每毫升血液中含药量y与时间t之间近似满足如图所示曲线:
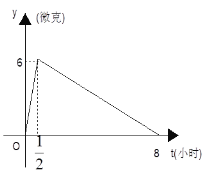
(1)分别求出![]() 和
和![]() 时,y与t之间的函数关系式;
时,y与t之间的函数关系式;
(2)据测定:每毫升血液中含药量不少于4微克时治疗疾病有效,假如某病人一天中第一次服药为7:00,那么服药后几点到几点有效?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com