
【题目】在□ABCD中,点E在CD上,点F在AB上,连接AE、CF、DF、BE,∠DAE=∠BCF.
(1)如图1,求证:四边形DFBE是平行四边形;
(2)如图2,若E是CD的中点,连接GH,在不添加任何辅助线的情况下,请直接写出图2中以GH为边或以GH为对角线的所有平行四边形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,点O是直线AB上一点,OD平分∠BOC,∠COE=90°.
(1)若∠AOC=36°,求∠DOE的度数;
(2)若∠AOC=α,则∠DOE=________.(用含α的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某开发区有一块四边形空地ABCD,现计划在空地上种植草皮,经测量,∠B=90°,AB=20m,BC=15m,CD=7m,AD=24m.若每平方米草皮需要200元,则种植这片草皮需要多少元?
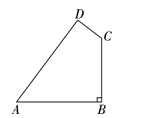
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极响应嘉兴市垃圾分类工作的号召,大力倡导低碳生活,保护我们的生存环境.某校按抽样规则抽取了部分学生进行垃圾分类的问卷调查(问卷内容如图1),答题情况如图2所示.


(1)参与本次问卷调查的学生共有多少人?
(2)若该校共有800名学生,则估计该校全体学生中对垃圾分类非常清楚(即“全对”)的人数有多少?
(3)为讲一步提高学生对垃圾分类的认识,学校加大了宣传,一个月后按同样的抽样规则抽取与第一次样本容量相等的学生进行第二次垃圾分类的问卷调查,答题情况如图3所示.求前后两次调查中答“全对”人数的增长率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲骑自行车从M地出发沿一条公路匀速前往N地,乙骑摩托车从N地出发沿同一条公路匀速前往M地,
已知乙比甲晚出发0.5小时且先到达目的地.设甲行驶的时间为t(h),甲乙两人之间的路程为y(km),
y与t的函数关系如图1所示,请解决以下问题:
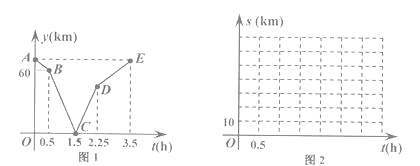
(1)写出图1中点C表示的实际意义并求线段BC所在直线的函数表达式.
(2)①求点D的纵坐标.
②求M,N两地之间的距离.
(3)设乙离M地的路程为S乙 (km),请直接写出S甲 与时间t(h)的函数表达式,并在图2所给的直角坐标系中画出它的图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,雯雯开了一家品牌手机体验店,想在体验区(图1阴影部分)摆放图2所示的正六边形桌子若干张.体验店平面图是长9米、宽7米的矩形,通道宽2米,桌子的边长为1米;摆放时要求桌子至少离墙1米,且有边与墙平行,桌子之间的最小距离至少1米,则体验区可以摆放桌子( )

A. 4张 B. 5张 C. 6张 D. 7张
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠MAN=120°,AC平分∠MAN,点B、D分别在AN、AM上.
(1)如图1,若∠ABC=∠ADC=90°,请你探索线段AD、AB、AC之间的数量关系,并证明之;
(2)如图2,若∠ABC+∠ADC=180°,则(1)中的结论是否仍然成立?若成立,给出证明;若不成立,请说明理由.
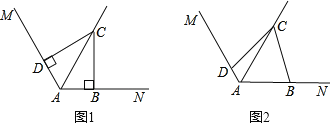
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一只拉杆式旅行箱(图1),其侧面示意图如图2所示.已知箱体长AB=50cm,拉杆![]() 的伸长距离最大时可达35cm,点A,B,C在同一条直线上.在箱体底端装有圆形的滚轮⊙A,⊙A与水平地面MN相切于点D.在拉杆伸长至最大的情况下,当点B距离水平地面38cm时,点C到水平地面的距离CE为59cm.
的伸长距离最大时可达35cm,点A,B,C在同一条直线上.在箱体底端装有圆形的滚轮⊙A,⊙A与水平地面MN相切于点D.在拉杆伸长至最大的情况下,当点B距离水平地面38cm时,点C到水平地面的距离CE为59cm.
设AF∥MN.
(1)求⊙A的半径长;
(2)当人的手自然下垂拉旅行箱时,人感到较为舒服.某人将手自然下垂在C端拉旅行箱时,CE为80cm,![]() =64°.求此时拉杆BC的伸长距离.(精确到1cm,参考数据:
=64°.求此时拉杆BC的伸长距离.(精确到1cm,参考数据:![]() ,
,![]() ,
,![]() )
)
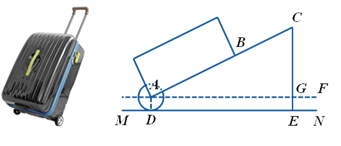
查看答案和解析>>
科目:初中数学 来源: 题型:
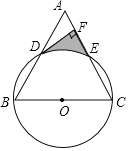
【题目】已知:如图,以等边△ABC的边BC为直径作⊙O,分别交AB,AC于点D,E,过点D作DF⊥AC交AC于点F.
(1)求证:DF是⊙O的切线;
(2)若等边△ABC的边长为8,求由![]() 、DF、EF围成的阴影部分面积.
、DF、EF围成的阴影部分面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com