
【题目】如图,某开发区有一块四边形空地ABCD,现计划在空地上种植草皮,经测量,∠B=90°,AB=20m,BC=15m,CD=7m,AD=24m.若每平方米草皮需要200元,则种植这片草皮需要多少元?
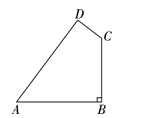
【答案】种植这片草皮需要234×200=46800元.
【解析】分析:先连接AC,根据勾股定理计算出AC,再根据勾股定理逆定理证明△ACD是直角三角形,然后根据面积公式计算.
详解:如图,连接AC,如图所示.
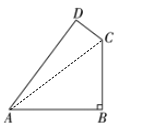
∵∠B=90°,AB=20m,BC=15m,
∴AC=![]() =25m.
=25m.
∵AC=25m,CD=7m,AD=24m,
∴AD2+DC2=AC2,
∴△ACD是直角三角形,且∠ADC=90°,
∴S△ABC=![]() ×AB×BC=
×AB×BC=![]() ×20×15=150m2,S△ACD=
×20×15=150m2,S△ACD=![]() ×CD×AD=
×CD×AD=![]() ×7×24=84m2,
×7×24=84m2,
∴S四边形ABCD=S△ABC+S△ACD=234m2.
所以种植这片草皮需要234×200=46800元.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中, AB的垂直平分线交AB于点D,AD=5cm,交边AC于点E,△BCE的周长等于18cm,则△ABC的周长等于( )
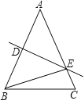
A. 23cmB. 25cmC. 28cmD. 30cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=kx+4图象交直线OA于点A(1,2),交y轴于点B,点C为坐标平面内一点.
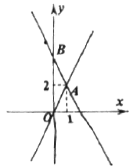
(1)求k值;
(2)若以O、A、B、C为顶点的四边形为菱形,则C点坐标为 ;
(3)在直线AB上找点D,使△OAD的面积与((2)中菱形面积相等,则D点坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠l=∠2,DE⊥BC,AB⊥BC,那么∠A=∠3吗?说明理由.

解:∠A=∠3,理由如下:
∵DE⊥BC,AB⊥BC(已知)
∴∠DEB=∠ABC=90° ( )
∴∠DEB+( )=180°
∴DE∥AB ( )
∴∠1=∠A( )
∠2=∠3( )
∵∠l=∠2(已知)
∴∠A=∠3( )
查看答案和解析>>
科目:初中数学 来源: 题型:
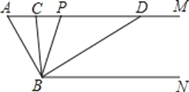
【题目】如图,已知AM∥BN,∠A=60°.点P是射线AM上一动点(与点A不重合),BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)求∠CBD的度数;
(2)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.
(3)当点P运动到使∠ACB=∠ABD时,直接写出∠ABC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将三角板ABC与三角板ADE摆放在一起;如图2,其中∠ACB=30°,∠DAE=45°,∠BAC=∠D=90°.固定三角板ABC,将三角板ADE绕点A按顺时针方向旋转,记旋转角∠CAE=α(0°<α<180°).
(1)当α为 度时,AD∥BC,并在图3中画出相应的图形;
(2)在旋转过程中,试探究∠CAD与∠BAE之间的关系;
(3)当△ADE旋转速度为5°/秒时,且它的一边与△ABC的某一边平行(不共线)时,直接写出时间t的所有值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=-3x与双曲线y=![]() 在第四象限内的部分相交于点A(a,-6),将这条直线向
在第四象限内的部分相交于点A(a,-6),将这条直线向
上平移后与该双曲线交于点M,且△AOM的面积为3.
(1)求k的值;
(2)求平移后得到的直线的函数表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在□ABCD中,点E在CD上,点F在AB上,连接AE、CF、DF、BE,∠DAE=∠BCF.
(1)如图1,求证:四边形DFBE是平行四边形;
(2)如图2,若E是CD的中点,连接GH,在不添加任何辅助线的情况下,请直接写出图2中以GH为边或以GH为对角线的所有平行四边形.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E,F是平行四边形ABCD对角线AC上两点,AE=CF=![]() AC.连接DE,DF并延长,分别交AB,BC于点G,H,连接GH,则
AC.连接DE,DF并延长,分别交AB,BC于点G,H,连接GH,则![]() 的值为( )
的值为( )
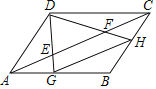
A. ![]() B.
B. ![]() C.
C. ![]() D. 1
D. 1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com