
【题目】如图,已知一次函数y=kx+4图象交直线OA于点A(1,2),交y轴于点B,点C为坐标平面内一点.
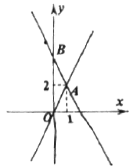
(1)求k值;
(2)若以O、A、B、C为顶点的四边形为菱形,则C点坐标为 ;
(3)在直线AB上找点D,使△OAD的面积与((2)中菱形面积相等,则D点坐标为 .
【答案】(1)k=-2;(2) (-1,2);(3)(-1,6)或(3,-2)
【解析】
(1)利用待定系数法即可解决问题;
(2)只要证明A、C关于y轴对称即可解决问题;
(3)分两种情形,根据AD=2AB即可解决问题;
(1)将点A(1,2)代入一次函数y=kx+4中,
2=k+4,得k=-2.
(2)∵一次函数解析式为y=-2x+4,
∴B点坐标为(0,4),∵A(1,2),
∴OA=![]() ,AB=
,AB=![]() ,
,
∵以O、A、B、C为顶点的四边形为菱形,
∴存在OB⊥AC,且OB、AC互相平分,由对称性得C点坐标为(-1,2).
故答案为(-1,2).
(3)∵四边形OABC是菱形,
∴S△OAB=![]() S菱形ABCO,
S菱形ABCO,
∴当AD=2AB时,△OAD的面积与(2)中菱形面积相等,
∵一次函数y=-2x+4与x轴的交点为(2,0),
∴D(-1,6)或(3,-2).


科目:初中数学 来源: 题型:
【题目】某汽车交易市场为了解二手轿车的交易情况,将本市场去年成交的二手轿车的全部数据,以二手轿车交易前的使用时间为标准分为A、B、C、D、E五类,并根据这些数据由甲,乙两人分别绘制了下面的两幅统计图(图都不完整).

请根据以上信息,解答下列问题:
(1)该汽车交易市场去年共交易二手轿车 辆.
(2)把这幅条形统计图补充完整.(画图后请标注相应的数据)
(3)在扇形统计图中,D类二手轿车交易辆数所对应扇形的圆心角为 度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 阅读下面的材料
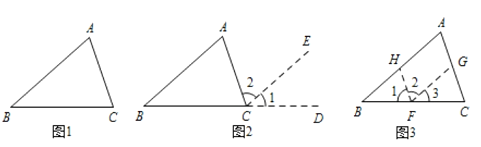
图1,在△ABC中,试说明∠A+∠B+∠C=180°
通过画平行线,将∠A、∠B、∠C作等量代换,使各角之和恰为一个平角,依辅助线不同而得多种方法:
解:如图2,延长BC到点D,过点C作CE∥BA
因为BA∥CE(作图所知)
所以∠B=∠2,∠A=∠1(两直线平行,同位角、内错角相等)
又因为∠BCD=∠BCA+∠2+∠1=180°(平角的定义)
所以∠A+∠B+∠ACB=180°(等量代换)
(1)如图3,过BC上任一点F,作FH∥AC,FG∥AB,这种添加辅助线的方法能说∠A+∠B+∠C=180°吗?并说明理由.
(2)还可以过点A作直线MN∥BC,或在三角形内取点P过P作三边的平行线,请选择一种方法,画出相应图形,并说明∠A+∠B+∠C=180°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是直线AB上一点,OD平分∠BOC,∠COE=90°.
(1)若∠AOC=36°,求∠DOE的度数;
(2)若∠AOC=α,则∠DOE=________.(用含α的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
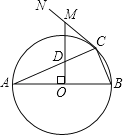
【题目】如图,AB是⊙O的直径,点C为⊙O上一点,CN为⊙O的切线,OM⊥AB于点O,分别交AC、CN于D、M两点.
(1)求证:MD=MC;
(2)若⊙O的半径为5,AC=4![]() ,求MC的长.
,求MC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据李飞与刘亮射击训练的成绩绘制了如图所示的折线统计图.

根据图所提供的信息,若要推荐一位成绩较稳定的选手去参赛,应推荐( )
A. 李飞或刘亮 B. 李飞 C. 刘亮 D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
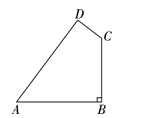
【题目】如图,某开发区有一块四边形空地ABCD,现计划在空地上种植草皮,经测量,∠B=90°,AB=20m,BC=15m,CD=7m,AD=24m.若每平方米草皮需要200元,则种植这片草皮需要多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
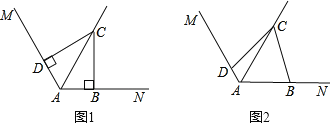
【题目】已知∠MAN=120°,AC平分∠MAN,点B、D分别在AN、AM上.
(1)如图1,若∠ABC=∠ADC=90°,请你探索线段AD、AB、AC之间的数量关系,并证明之;
(2)如图2,若∠ABC+∠ADC=180°,则(1)中的结论是否仍然成立?若成立,给出证明;若不成立,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com