
【题目】 阅读下面的材料
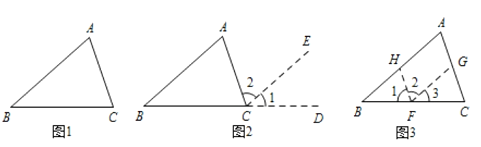
图1,在△ABC中,试说明∠A+∠B+∠C=180°
通过画平行线,将∠A、∠B、∠C作等量代换,使各角之和恰为一个平角,依辅助线不同而得多种方法:
解:如图2,延长BC到点D,过点C作CE∥BA
因为BA∥CE(作图所知)
所以∠B=∠2,∠A=∠1(两直线平行,同位角、内错角相等)
又因为∠BCD=∠BCA+∠2+∠1=180°(平角的定义)
所以∠A+∠B+∠ACB=180°(等量代换)
(1)如图3,过BC上任一点F,作FH∥AC,FG∥AB,这种添加辅助线的方法能说∠A+∠B+∠C=180°吗?并说明理由.
(2)还可以过点A作直线MN∥BC,或在三角形内取点P过P作三边的平行线,请选择一种方法,画出相应图形,并说明∠A+∠B+∠C=180°.
科目:初中数学 来源: 题型:
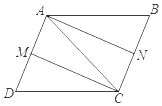
【题目】已知:如图,在平行四边形ABCD中,M、N分别是AD和BC的中点.
(1)求证:四边形AMCN是平行四边形;
(2)若AC=CD,求证四边形AMCN是矩形;
(3)若∠ACD=90°,求证四边形AMCN是菱形;
(4)若AC=CD,∠ACD=90°,求证四边形AMCN是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中, AB的垂直平分线交AB于点D,AD=5cm,交边AC于点E,△BCE的周长等于18cm,则△ABC的周长等于( )
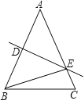
A. 23cmB. 25cmC. 28cmD. 30cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.
(1)求证:AB=CD;
(2)若AB=CF,∠B=30°,求∠D的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,如果∠ABP=20°,∠ACP=50°,则∠A+∠P=( )

A.70°B.80°C.90°D.100°
查看答案和解析>>
科目:初中数学 来源: 题型:
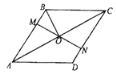
【题目】如图,在菱形ABCD中,点M、 N分别在AB、CD上,AM=CN, MN与AC交于点O,连接BO,若∠BAC=29°,则∠OBC为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=kx+4图象交直线OA于点A(1,2),交y轴于点B,点C为坐标平面内一点.
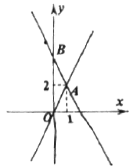
(1)求k值;
(2)若以O、A、B、C为顶点的四边形为菱形,则C点坐标为 ;
(3)在直线AB上找点D,使△OAD的面积与((2)中菱形面积相等,则D点坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=-3x与双曲线y=![]() 在第四象限内的部分相交于点A(a,-6),将这条直线向
在第四象限内的部分相交于点A(a,-6),将这条直线向
上平移后与该双曲线交于点M,且△AOM的面积为3.
(1)求k的值;
(2)求平移后得到的直线的函数表达式.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com