练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，BP是△ABC中∠ABC的平分线，CP是∠ACB的外角的平分线，如果∠ABP=20°，∠ACP=50°，则∠A+∠P=（ ）

    A.70°B.80°C.90°D.100°

    【答案】C

    【解析】

    根据角平分线的定义以及一个三角形的外角等于与它不相邻的两个内角和，可求出∠A的度数，根据补角的定义求出∠ACB的度数，根据三角形的内角和即可求出∠P的度数，即可求出结果．

    解：∵BP是△ABC中∠ABC的平分线，CP是∠ACB的外角的平分线，

    ∵∠ABP=20°，∠ACP=50°，

    ∴∠ABC=2∠ABP=40°，∠ACM=2∠ACP=100°，

    ∴∠A=∠ACM-∠ABC=60°，

    ∠ACB=180°-∠ACM=80°，

    ∴∠BCP=∠ACB+∠ACP=130°，

    ∵∠BPC=20°，

    ∴∠P=180°-∠PBC-∠BCP=30°，

    ∴∠A+∠P=90°，

    故选：C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】为了解市民对“垃圾分类知识”的知晓程度,某数学学习兴趣小组对市民进行随机抽样的问卷调查,调查结果分为“.非常了解”、“.了解”、“.基本了解”、“.不太了解”四个等级进行统计,并将统计结果绘制成如下两幅不完整的统计图(图1,图2),请根据图中的信息解答下列问题.

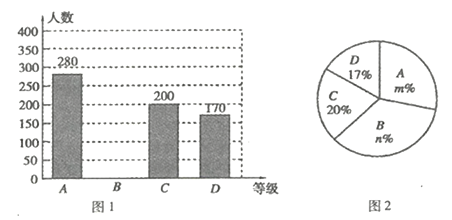
    (1)这次调查的市民人数为 人,图2中, ；

    (2)补全图1中的条形统计图；

    (3)在图2中的扇形统计图中,求“.基本了解”所在扇形的圆心角度数；

    (4)据统计,2018年该市约有市民500万人,那么根据抽样调查的结果,可估计对“垃圾分类知识”的知晓程度为“.不太了解”的市民约有多少万人？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，小蚂蚁在9×9的小方格上沿着网格线运动（每小格边长为1），一只蚂蚁在C处找到食物后，要通知A、B、D、E处的其他小蚂蚁，我们把它的行动规定：向上或向右为正，向下或向左为负。如果从C到D记为：C→D（＋2，－3）（第一个数表示左、右方向，第二个数表示上、下方向），那么；

    （1）C→B（　　　），C→E（　　　），D→ （－4，－3），D→ （ ，＋3）；

    （2）若这只小蚂蚁的行走路线为C→E→D→B→A→C，请你计算小蚂蚁走过的路程．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】将一幅三角板拼成如图所示的图形，过点C作CF平分∠DCE交DE于点F．

    （1）求证：CF∥AB．

    （2）求∠DFC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】 阅读下面的材料

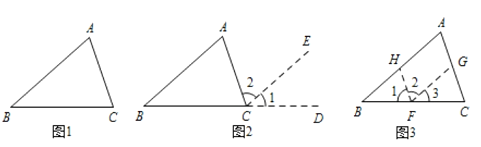
    图1，在△ABC中，试说明∠A+∠B+∠C=180°

    通过画平行线，将∠A、∠B、∠C作等量代换，使各角之和恰为一个平角，依辅助线不同而得多种方法：

    解：如图2，延长BC到点D，过点C作CE∥BA

    因为BA∥CE（作图所知）

    所以∠B=∠2，∠A=∠1（两直线平行，同位角、内错角相等）

    又因为∠BCD=∠BCA+∠2+∠1=180°（平角的定义）

    所以∠A+∠B+∠ACB=180°（等量代换）

    （1）如图3，过BC上任一点F，作FH∥AC，FG∥AB，这种添加辅助线的方法能说∠A+∠B+∠C=180°吗？并说明理由．

    （2）还可以过点A作直线MN∥BC，或在三角形内取点P过P作三边的平行线，请选择一种方法，画出相应图形，并说明∠A+∠B+∠C=180°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AD为△ABC的中线，BE为△ABD的中线．

    (1)若∠ABE＝15°，∠BAD＝40°，则∠BED＝________°；

    (2)请在图中作出△BED中BD边上的高EF；

    (3)若△ABC的面积为40，BD＝5，则点E到BC边的距离为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点O是直线AB上一点，OD平分∠BOC，∠COE＝90°.

    (1)若∠AOC＝36°，求∠DOE的度数；

    (2)若∠AOC＝α，则∠DOE＝________.(用含α的代数式表示)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】根据李飞与刘亮射击训练的成绩绘制了如图所示的折线统计图．

    根据图所提供的信息，若要推荐一位成绩较稳定的选手去参赛，应推荐（　　）

    A. 李飞或刘亮 B. 李飞 C. 刘亮 D. 无法确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为积极响应嘉兴市垃圾分类工作的号召，大力倡导低碳生活，保护我们的生存环境．某校按抽样规则抽取了部分学生进行垃圾分类的问卷调查(问卷内容如图1)，答题情况如图2所示．

    （1）参与本次问卷调查的学生共有多少人?

    （2）若该校共有800名学生，则估计该校全体学生中对垃圾分类非常清楚(即“全对”)的人数有多少?

    （3）为讲一步提高学生对垃圾分类的认识，学校加大了宣传，一个月后按同样的抽样规则抽取与第一次样本容量相等的学生进行第二次垃圾分类的问卷调查，答题情况如图3所示．求前后两次调查中答“全对”人数的增长率．

    查看答案和解析>>

    同步练习册答案