
【题目】为了解市民对“垃圾分类知识”的知晓程度,某数学学习兴趣小组对市民进行随机抽样的问卷调查,调查结果分为“![]() .非常了解”、“
.非常了解”、“![]() .了解”、“
.了解”、“![]() .基本了解”、“
.基本了解”、“![]() .不太了解”四个等级进行统计,并将统计结果绘制成如下两幅不完整的统计图(图1,图2),请根据图中的信息解答下列问题.
.不太了解”四个等级进行统计,并将统计结果绘制成如下两幅不完整的统计图(图1,图2),请根据图中的信息解答下列问题.
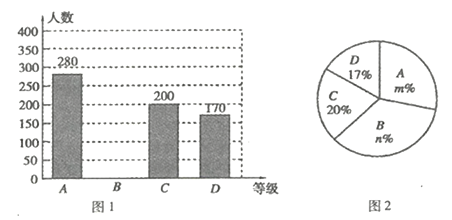
(1)这次调查的市民人数为 人,图2中, ![]() ;
;
(2)补全图1中的条形统计图;
(3)在图2中的扇形统计图中,求“![]() .基本了解”所在扇形的圆心角度数;
.基本了解”所在扇形的圆心角度数;
(4)据统计,2018年该市约有市民500万人,那么根据抽样调查的结果,可估计对“垃圾分类知识”的知晓程度为“![]() .不太了解”的市民约有多少万人?
.不太了解”的市民约有多少万人?
【答案】(1)1000,35;(2)画图见解析;(3)![]() ;(4)85万人.
;(4)85万人.
【解析】
(1)根据C类的人数和所占的百分比求出调查的总人数,再根据A类的人数求出A类所占的百分比,从而求出n的值;
(2)根据求出的总人数和B类所占的百分比即可求出B类的人数,从而补全统计图;
(3)用360°乘以“C.基本了解”所占的百分比即可;
(4)用2018年该市约有的市民乘以“D不太了解”所占的百分比即可得出答案.
(1)这次调查的市民人数为:20÷20%=1000(人);
∵m%=![]() ×100%=28%,
×100%=28%,
n%=1-20%-17%-28%=35%,
∴n=35;
故答案为:1000,35;
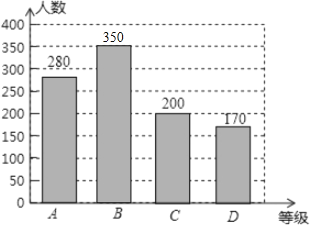
(2)B等级的人数是:1000×35%=350(人),补图如下:
(3)基本了解”所在扇形的圆心角度数为:360°×20%=72°;
故答案为:72;
(4)根据题意得:
500×17%=85(万人),
答:估计对“垃圾分类知识”的知晓程度为“D.不太了解”的市民约有85万人.


科目:初中数学 来源: 题型:
【题目】某校积极开展“阳光体育进校园”活动,决定开设 A:乒乓球,B:篮球,C:跑步,D:跳绳四种运动项目,规定每个学生必须参加一项活动。学校为了了解学生最喜欢哪一种运动项目,设计了以下四种调查方案.
方案一:调查该校七年级女生喜欢的运动项目
方案二:调查该校每个班级学号为 5 的倍数的学生喜欢的运动项目
方案三:调查该校书法小组的学生喜欢的运动项目
方案四:调查该校田径队的学生喜欢的运动项目
(1)上面的调查方案最合适的是 ;
学校体育组采用了(1)中的方案,将调查的结果绘制成如下两幅不完整的统计图表.
最喜欢的运动项目人数调查统计表 最喜欢的运动项目人数分布统计图
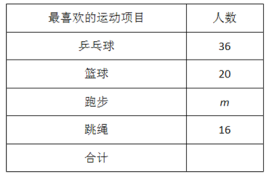
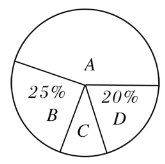
请你结合图表中的信息解答下列问题:
(2)这次抽样调查的总人数是 ,m= ;
(3)在扇形统计图中,A 项目对应的圆心角的度数为 ;
(4)已知该校有 1200 名学生,请根据调查结果估计全校学生最喜欢乒乓球的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解学生对体育活动的喜爱情况,某校对参加足球、篮球、乒乓球、羽毛球这四个课外活动小组的人员分布情况进行抽样调査,并根据收集的数据绘制了下面两幅不完整的统计图,请根据图中提供的信息,解答下面问题.

(1)此次共调査了________名同学,扇形统计图中的篮球部分所占的圆心角的度数是______;
(2)直接将条形统计图补充完整;
(3)如果该校共有1000名学生参加这四个课外活动小组,而每个教师最多只能辅导本组的20名学生,请通过计算确定学校需要为乒乓球课外活动小组至少准备多少名教师?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D、E在△ABC的BC边上,BD=CE,AD=AE。

(1)如图1,求证:∠BAD=∠CAE;
(2)如图2,若点E在AC的垂直平分线上,∠C=36°,直接写出图中所有的等腰三角形。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据研究弹簧长度与重物重量的实验表格,下列说法错误的是( )

A. 自变量是重物重量x,因变量是弹簧长度yB. 弹簧原长8cm
C. 重物重量每增加1kg,弹簧长度伸长4cmD. 当悬挂重物重量为6kg时,弹簧伸长12cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,一次函数y=kx﹣1的图象经过点A(3![]() ,m)(m>0),与y轴交于点B.点C在线段AB上,且BC=2AC,过点C作x轴的垂线,垂足为点D.若AC=CD.
,m)(m>0),与y轴交于点B.点C在线段AB上,且BC=2AC,过点C作x轴的垂线,垂足为点D.若AC=CD.
(1)求这个一次函数的表达式;
(2)已知一开口向下、以直线CD为对称轴的抛物线经过点A,它的顶点为P,若过点P且垂直于AP的直线与x轴的交点为Q(﹣![]() ,0),求这条抛物线的函数表达式.
,0),求这条抛物线的函数表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,如果∠ABP=20°,∠ACP=50°,则∠A+∠P=( )

A.70°B.80°C.90°D.100°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com