
【题目】如图,点D、E在△ABC的BC边上,BD=CE,AD=AE。

(1)如图1,求证:∠BAD=∠CAE;
(2)如图2,若点E在AC的垂直平分线上,∠C=36°,直接写出图中所有的等腰三角形。
【答案】(1)见解析(2)△ABC,△ABD,△ADE,△ACE,△ACD,△ABE
【解析】
(1)根据AD=AE得到△ADE是等腰三角形,得到∠ADE=∠AED,根据平角的性质得到∠ADB=∠AEC,又BD=CE,可证明△ADB≌△AEC,故可求解;
(2)由(1)可得AB=AC,根据点E在AC的垂直平分线上得到AE=CE,故AD=DE,根据等腰三角形的定义即可写出.
(1)∵AD=AE
∴△ADE是等腰三角形,
∴∠ADE=∠AED,
∴∠ADB=∠AEC,
又BD=CE,
∴△ADB≌△AEC
∴∠BAD=∠CAE;
(2)∵△ADB≌△AEC
∴AB=AC,
∵点E在AC的垂直平分线上
∴AE=CE,∴BD=AD
∵∠C=36°,∴∠AED=2∠C=72°,
∴ADE=72°,
∴∠DAE=180°-2∠AED=36°,
∴∠CAD=∠DAE+∠CAE=72°,
∴AC=CD
同理AB=BE
∴图中的等腰三角形有△ABC,△ABD,△ADE,△ACE,△ACD,△ABE.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
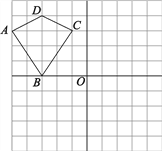
【题目】下面方格中有一个四边形ABCD和点O,请在方格中画出以下图形(只要求画出平移、旋转后的图形,不要求写出作图步骤和过程).
(1)画出四边形ABCD以点O为旋转中心,逆时针旋转90°后得到的四边形A1B1C1D1;
(2)画出四边形A1B1C1D1向右平移3格(3个小方格的边长)后得到的四边形A2B2C2D2;
(3)填空:若每个小方格的边长为1,则四边形A1B1C1D1与四边形A2B2C2D2重叠部分的面积为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中放有四张卡片,每张卡片上写有一个实数,分别为2,![]() ,
,![]() ,1.(卡片除了实数不同外,其余均相同)
,1.(卡片除了实数不同外,其余均相同)
(1)从盒子中随机抽取一张卡片,请直接写出卡片上的实数是有理数的概率;
(2)将卡片揺匀后先随机抽出一张,再从剩下的卡片中随机抽出一张,然后将抽取的两张卡片上的实数相乘,请你用列表法或树状图(树形图)法,求抽取的两张卡片上的实数之积为整数的概率。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】建设中的大外环路是我市的一项重点民生工程.某工程公司承建的一段路基工程的施工土方量为120万立方,原计划由公司的甲、乙两个工程队从公路的两端同时相向施工150天完成.由于特殊情况需要,公司抽调甲队外援施工,由乙队先单独施工40天后甲队返回,两队又共同施工了110天,这时甲乙两队共完成土方量103.2万立方.
(1)问甲、乙两队原计划平均每天的施工土方量分别为多少万立方?
(2)在抽调甲队外援施工的情况下,为了保证150天完成任务,公司为乙队新购进了一批机械来提高效率,那么乙队平均每天的施工土方量至少要比原来提高多少万立方才能保证按时完成任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解市民对“垃圾分类知识”的知晓程度,某数学学习兴趣小组对市民进行随机抽样的问卷调查,调查结果分为“![]() .非常了解”、“
.非常了解”、“![]() .了解”、“
.了解”、“![]() .基本了解”、“
.基本了解”、“![]() .不太了解”四个等级进行统计,并将统计结果绘制成如下两幅不完整的统计图(图1,图2),请根据图中的信息解答下列问题.
.不太了解”四个等级进行统计,并将统计结果绘制成如下两幅不完整的统计图(图1,图2),请根据图中的信息解答下列问题.
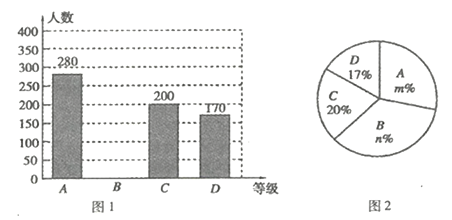
(1)这次调查的市民人数为 人,图2中, ![]() ;
;
(2)补全图1中的条形统计图;
(3)在图2中的扇形统计图中,求“![]() .基本了解”所在扇形的圆心角度数;
.基本了解”所在扇形的圆心角度数;
(4)据统计,2018年该市约有市民500万人,那么根据抽样调查的结果,可估计对“垃圾分类知识”的知晓程度为“![]() .不太了解”的市民约有多少万人?
.不太了解”的市民约有多少万人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,D、E分别是边AB、BC上的点,AE和CD交于点F,且∠CFE=∠B。
(1)如图1,求证:∠AEC=∠CDB;

(2)如图2,过点C作CG⊥AC,交AB于点G,CD⊥CB,∠ACD =∠CAB-∠B,求证:AC=GC;

(3)如图3,在(2)的条件下,CE+CD=AE,CG=![]() ,求线段BC的长。
,求线段BC的长。

查看答案和解析>>
科目:初中数学 来源: 题型:
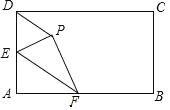
【题目】如图,在矩形ABCD中,AB=8,AD=4,点E、F分别在线段AD、AB上,将△AEF沿EF翻折,使得点A落在矩形ABCD内部的P点,连接PD,当△PDE是等边三角形时,BF的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知港口A东偏南10°方向有一处小岛B,一艘货轮从港口A沿南偏东40°航线出发,行驶80海里到达C处,此时观测小岛B在北偏东60°方向.
(1)求此时货轮到小岛B的距离.
(2)在小岛周围36海里范围内是暗礁区,此时轮船向正东方向航行有没有触礁危险?请作出判断并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD为△ABC的中线,BE为△ABD的中线.
(1)若∠ABE=15°,∠BAD=40°,则∠BED=________°;
(2)请在图中作出△BED中BD边上的高EF;
(3)若△ABC的面积为40,BD=5,则点E到BC边的距离为多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com