
【题目】建设中的大外环路是我市的一项重点民生工程.某工程公司承建的一段路基工程的施工土方量为120万立方,原计划由公司的甲、乙两个工程队从公路的两端同时相向施工150天完成.由于特殊情况需要,公司抽调甲队外援施工,由乙队先单独施工40天后甲队返回,两队又共同施工了110天,这时甲乙两队共完成土方量103.2万立方.
(1)问甲、乙两队原计划平均每天的施工土方量分别为多少万立方?
(2)在抽调甲队外援施工的情况下,为了保证150天完成任务,公司为乙队新购进了一批机械来提高效率,那么乙队平均每天的施工土方量至少要比原来提高多少万立方才能保证按时完成任务?
【答案】(1)甲、乙两队原计划平均每天的施工土方量分别为0.42万立方和0.38万立方.(2)乙队平均每天的施工土方量至少要比原来提高0.112万立方才能保证按时完成任务.
【解析】分析: (1)设甲队原计划平均每天的施工土方量为x万立方,乙队原计划平均每天的施工土方量为y万立方,根据“甲乙两队合作150天完成土方量120万立方,甲队施工110天、乙队施工150天完成土方量103.2万立方”,即可得出关于x、y的二元一次方程组,解之即可得出结论;
(2)设乙队平均每天的施工土方量比原来提高a万立方才能保证按时完成任务,根据完成工作的总量=甲队完成的土方量+乙队完成的土方量,即可得出关于a的一元一次不等式,解之取其中的最小值即可得出结论.
详解:
(1)设甲队原计划平均每天的施工土方量为x万立方,乙队原计划平均每天的施工土方量为y万立方.根据题意,得
![]()
解之,得![]()
答:甲、乙两队原计划平均每天的施工土方量分别为0.42万立方和0.38万立方.
(2)设乙队平均每天的施工土方量至少要比原来提高z万立方.根据题意,得
40(0.38+z)+110(0.38+z+0.42≥120,
解之,得z≥0.112,
答:乙队平均每天的施工土方量至少要比原来提高0.112万立方才能保证按时完成任务.


科目:初中数学 来源: 题型:
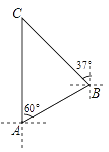
【题目】知识改变世界,科技改变生活.导航装备的不断更新极大方便了人们的出行.如图,某校组织学生乘车到黑龙滩(用C表示)开展社会实践活动,车到达A地后,发现C地恰好在A地的正北方向,且距离A地13千米,导航显示车辆应沿北偏东60°方向行驶至B地,再沿北偏西37°方向行驶一段距离才能到达C地,求B、C两地的距离.(参考数据:sin53°≈![]() ,cos53°≈
,cos53°≈![]() ,tan53°≈
,tan53°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的两边OA,OC分别在x轴和y轴上,并且OA=5,OC=3.若把矩形OABC绕着点O逆时针旋转,使点A恰好落在BC边上的A1处,则点C的对应点C1的坐标为( )
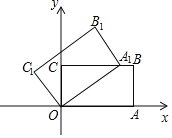
A. (﹣![]() ) B. (﹣
) B. (﹣![]() ) C. (﹣
) C. (﹣![]() ) D. (﹣
) D. (﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,给出五个等量关系:①AD=BC;②AC=BD;③CE=DE;④∠D=∠C;⑤∠DAB=∠CBA.
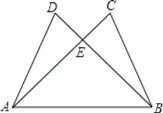
请你以其中两个为条件,另外三个中的一个为结论,推出一个正确的结论(只需写出一种情况),并加以证明.
已知:
求证:
证明:
查看答案和解析>>
科目:初中数学 来源: 题型:
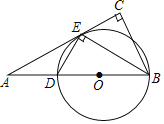
【题目】如图,在Rt△ABC中,∠C=90°,BE平分∠ABC交AC于点E,作ED⊥EB交AB于点D,⊙O是△BED的外接圆.
(1)求证:AC是⊙O的切线;
(2)已知⊙O的半径为2.5,BE=4,求BC,AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:用分离系数法进行整式的加减运算.
我们已经学过整式的加减,而我们可以列竖式进行整式的加减运算,只要将参加运算的整式连同字母进行降幂排列,凡缺项则留出空位或添零,然后让常数项对齐(即右对齐)即可.例如,计算(x3﹣2x2﹣5)﹣(x﹣2x2﹣1)时,我们可以用下列竖式计算:
竖式:
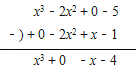
(x3﹣2x2+5)﹣(x﹣2x2﹣1)=x3﹣x﹣4
这种方法叫做分离系数法.用分离系数法计算:
(1)(2x2+4x﹣3)+(5﹣4x+x2);
(2)(3y3﹣5y2﹣6)﹣(y﹣2+3y3).
查看答案和解析>>
科目:初中数学 来源: 题型:
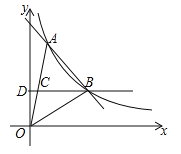
【题目】(2017山东省菏泽市,第20题,7分)如图,一次函数y=kx+b与反比例函数![]() 的图象在第一象限交于A、B两点,B点的坐标为(3,2),连接OA、OB,过B作BD⊥y轴,垂足为D,交OA于C,若OC=CA.
的图象在第一象限交于A、B两点,B点的坐标为(3,2),连接OA、OB,过B作BD⊥y轴,垂足为D,交OA于C,若OC=CA.
(1)求一次函数和反比例函数的表达式;
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
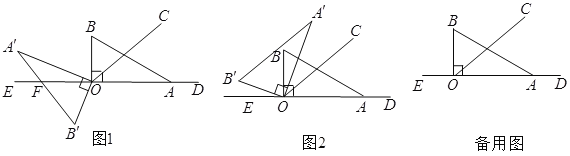
【题目】直线DE上有一点O,过点O在直线DE上方作射线OC,将直角三角板AOB(∠OAB=30°)的直角顶点放在点O处,一条直角边OA在射线OD上,另一边OB在直线DE上方.将直角三角板绕点O按每秒10°的速度逆时针旋转得到三角形A'OB',三角形AOB旋转一周后停止旋转,设旋转时间为t秒.若射线OC的位置保持不变,∠COD=40°.
(1)如图1,在旋转过程中,当边A'B'与直线DE相交于点F时,请用含t的代数式分别表示∠A'OC和∠B'OF的度数,并求出∠A'OC-∠B'OF的值;
(2)如图2,当t=7时,试说明直线A'B'//OC;
(3)在旋转过程中,若t=7,是否还存在某一时刻,使得A'B'//OC;若存在,请求出符合条件的t值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com