
【题目】直线DE上有一点O,过点O在直线DE上方作射线OC,将直角三角板AOB(∠OAB=30°)的直角顶点放在点O处,一条直角边OA在射线OD上,另一边OB在直线DE上方.将直角三角板绕点O按每秒10°的速度逆时针旋转得到三角形A'OB',三角形AOB旋转一周后停止旋转,设旋转时间为t秒.若射线OC的位置保持不变,∠COD=40°.
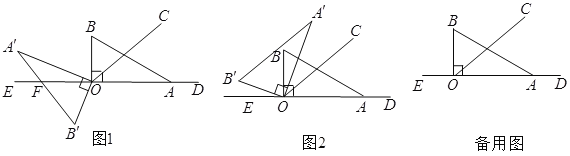
(1)如图1,在旋转过程中,当边A'B'与直线DE相交于点F时,请用含t的代数式分别表示∠A'OC和∠B'OF的度数,并求出∠A'OC-∠B'OF的值;
(2)如图2,当t=7时,试说明直线A'B'//OC;
(3)在旋转过程中,若t=7,是否还存在某一时刻,使得A'B'//OC;若存在,请求出符合条件的t值;若不存在,请说明理由.
【答案】∠A′OC=10°t-40°,∠B′OF=10°t-90°,50°;(2)详见解析;(3)t=25.
【解析】
(1)根据∠A′OC=∠A′OD-∠COD,∠B′OF=∠B'OB-∠BOF用含t的式子表示出∠A'OC,∠B′OF,然后计算∠A'OC﹣∠B′OF即可;
(2)把t=7代入∠A′OC的表达式,求出∠A′OC的度数,得到∠A′OC=∠A′,根据内错角相等,两直线平行即可得到结论;
(3)根据同旁内角互补,两直线平行,当∠A′OC+∠A′=180°时,A′B′∥OC,列方程得:360°-(10°t-40°)+30°=180°,求解即可.
(1)∠A′OC=∠A′OD-∠COD=10°t-40°,∠B′OF=∠B'OB-∠BOF=10°t-90°,
∠A'OC﹣∠B′OF=(10°t-40°)-(10°t-90°)=50°.
(2)因为t=7,所以∠A′OC=10°×7-40°=30°,
因为∠A′=∠A=30°,
所以∠A′OC=∠A′,
所以A′B′∥OC;(内错角相等,两直线平行)
(3)如图,
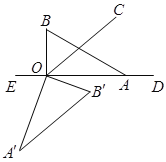
当∠A′OC+∠A′=180°时,
A′B′∥OC,(同旁内角互补,两直线平行)
所以360°-(10°t-40°)+30°=180°,
解得:t=25.


科目:初中数学 来源: 题型:
【题目】建设中的大外环路是我市的一项重点民生工程.某工程公司承建的一段路基工程的施工土方量为120万立方,原计划由公司的甲、乙两个工程队从公路的两端同时相向施工150天完成.由于特殊情况需要,公司抽调甲队外援施工,由乙队先单独施工40天后甲队返回,两队又共同施工了110天,这时甲乙两队共完成土方量103.2万立方.
(1)问甲、乙两队原计划平均每天的施工土方量分别为多少万立方?
(2)在抽调甲队外援施工的情况下,为了保证150天完成任务,公司为乙队新购进了一批机械来提高效率,那么乙队平均每天的施工土方量至少要比原来提高多少万立方才能保证按时完成任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
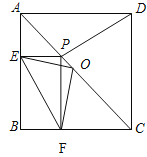
【题目】如图,已知:在正方形ABCD中,点P在AC上,PE⊥AB于E,PF⊥BC于F.
(1)试判断线段EF与PD的长是否相等,并说明理由.
(2)若点O是AC的中点,判断OF与OE之间有怎样的位置和数量关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】多项式4x2+1加上一个单项式,使它成为一个整式的完全平方,则这个单项式可以是__________________.(填写符合条件的一个即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场第1次用39万元购进A、B两种商品,销售完后获得利润6万元,它们的进价和售价如下表:(总利润=单件利润×销售量)
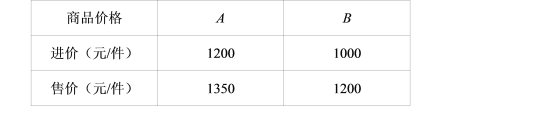
(1)该商场第1次购进A、B两种商品各多少件?
(2)商场第2次以原价购进A、B两种商品,购进A商品的件数不变,而购进B商品的件数是第1次的2倍,A商品按原价销售,而B商品打折销售,若两种商品销售完毕,要使得第2次经营活动获得利润等于54000元,则B种商品是打几折销售的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一组有规律的图案,它们是由边长相同的正方形和正三角形拼接而成,第①个图案有4个三角形和1个正方形,第②个图案有7个三角形和2个正方形,第③个图案有10个三角形和3个正方形,…依此规律,第n个图案有 ____________个三角形(用含n的代数式表示);

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极响应“弘扬传统文化”的号召,某学校倡导全校1200名学生进行经典诗词诵背活动,并在活动之后举办经典诗词大赛,为了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取部分学生调查“一周诗词诵背数量”,根调查结果绘制成的统计图(部分)如图所示.
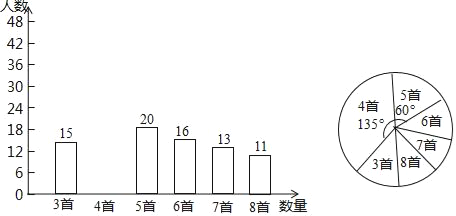
大赛结束后一个月,再次抽查这部分学生“一周诗词诵背数量”,绘制成统计表
一周诗词诵背数量 | 3首 | 4首 | 5首 | 6首 | 7首 | 8首 |
人数 | 10 | 10 | 15 | 40 | 25 | 20 |
请根据调查的信息
(1)活动启动之初学生“一周诗词诵背数量”的中位数为 ;
(2)估计大赛后一个月该校学生一周诗词诵背6首(含6首)以上的人数;
(3)选择适当的统计量,从两个不同的角度分析两次调查的相关数据,评价该校经典诗词诵背系列活动的效果.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com