
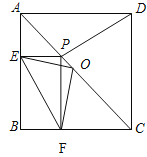
【题目】如图,已知:在正方形ABCD中,点P在AC上,PE⊥AB于E,PF⊥BC于F.
(1)试判断线段EF与PD的长是否相等,并说明理由.
(2)若点O是AC的中点,判断OF与OE之间有怎样的位置和数量关系?并说明理由.
【答案】(1)相等,理由见解析;(2)OF与OE垂直且相等,理由见解析.
【解析】试题分析:(1)连接BP,易证四边形EPFB是矩形,由矩形的性质即可证明EF=PD;
(2)OF与OE垂直且相等,连接BO,证明△EBO与△FCO全等即可.
解:(1)EF=PD,理由如下:
连接BP,
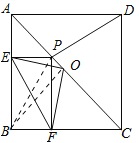
∵四边形ABCD是正方形,
∴∠ABC=90°,AD=AB,∠DAP=∠BAP=45°,
在△BAP和△DAP中,
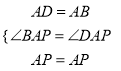 ,
,
∴PD=PB,
∵PE⊥AB于E,PF⊥BC于F,
∴∠PEB=∠PFB=90°,
∴四边形EPFB是矩形,
∴EF=PB,
∴EF=PD;
(2)OF与OE垂直且相等,理由如下:
连接BO,

∵点O是AC的中点,
∴∠EBO=∠FCO=45°,
∵BF=EP,AE=EP,
∴AE=BF,
∴BE=CF,
在△EBO和△FCO中
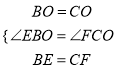 ,
,
∴△EBO≌△FCO,
∴OE=OF,∠EOB=∠COF,
∵OB⊥AC,
∴∠BOC=90°,
∴∠COF+∠BOF=90°,
∴∠EOB+∠BOF=90°,
即OE⊥OF.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,CA=8,CB=6,动点P从C出发沿CA方向,以每秒1个单位长度的速度向A点匀速运动,到达A点后立即以原来速度沿AC返回;同时动点Q从点A出发沿AB以每秒1个单位长度向点B匀速运动,当Q到达B时,P、Q两点同时停止运动.设P、Q运动的时间为t秒(t>0).
(1)当t为何值时,PQ∥CB?
(2)在点P从C向A运动的过程中,在CB上是否存在点E使△CEP与△PQA全等?若存在,求出CE的长;若不存在,请说明理由;
(3)伴随着P、Q两点的运动,线段PQ的垂直平分线DF交PQ于点D,交折线QB﹣BC﹣CP于点F.当DF经过点C时,求出t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CB=CA,∠ACB=90°,点D在边BC上(与B,C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:①AC=FG;②S△FAB∶S四边形CBFG=1∶2;③∠ABC=∠ABF;④AD2=FQ·AC,其中正确结论的个数是( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为建设“美丽乡村”,需要对某村居民的自来水管进行改造,该工程若由甲队单独施工恰好在规定时间内完成;若由乙队单独施工,则完成工程所需时间是规定天数的1.5倍如果由甲、乙两队先合做10天,那么余下的工程由乙队单独完成还需5天.
(1)这项工程完成规定的时间是多少天?
(2)已知甲队每天的施工费用为6500元,乙队每天的施工费用为3600元,为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙两队合做来完成,则该工程施工费用是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com