
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯACB=90ЁуЃЌCA=8ЃЌCB=6ЃЌЖЏЕуPДгCГіЗЂбиCAЗНЯђЃЌвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШЯђAЕудШЫйдЫЖЏЃЌЕНДяAЕуКѓСЂМДвддРДЫйЖШбиACЗЕЛиЃЛЭЌЪБЖЏЕуQДгЕуAГіЗЂбиABвдУПУы1ИіЕЅЮЛГЄЖШЯђЕуBдШЫйдЫЖЏЃЌЕБQЕНДяBЪБЃЌPЁЂQСНЕуЭЌЪБЭЃжЙдЫЖЏЃЎЩшPЁЂQдЫЖЏЕФЪБМфЮЊtУыЃЈtЃО0ЃЉЃЎ
ЃЈ1ЃЉЕБtЮЊКЮжЕЪБЃЌPQЁЮCBЃП
ЃЈ2ЃЉдкЕуPДгCЯђAдЫЖЏЕФЙ§ГЬжаЃЌдкCBЩЯЪЧЗёДцдкЕуEЪЙЁїCEPгыЁїPQAШЋЕШЃПШєДцдкЃЌЧѓГіCEЕФГЄЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉАщЫцзХPЁЂQСНЕуЕФдЫЖЏЃЌЯпЖЮPQЕФДЙжБЦНЗжЯпDFНЛPQгкЕуDЃЌНЛелЯпQBЉBCЉCPгкЕуFЃЎЕБDFОЙ§ЕуCЪБЃЌЧѓГіtЕФжЕЃЎ

ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉДцдкЃЌ
ЃЛЃЈ2ЃЉДцдкЃЌ![]() ЃЛЃЈ3ЃЉ5КЭ10.
ЃЛЃЈ3ЃЉ5КЭ10.
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉИљОнЙДЙЩЖЈРэЧѓГіABЃЌИљОнЦНааЯпЗжЯпЖЮГЩБШР§ЖЈРэСаГіБШР§ЪНЃЌМЦЫуМДПЩЃЛ
ЃЈ2ЃЉИљОнШЋЕШШ§НЧаЮЕФаджЪЕУЕНЁЯPQA=90ЁуЃЌИљОнЯрЫЦШ§НЧаЮЕФаджЪЧѓГіPEЃЌИљОнЙДЙЩЖЈРэМЦЫуЃЛ
ЃЈ3ЃЉЗжPгЩCЯђAдЫЖЏКЭPгЩAЯђCдЫЖЏСНжжЧщПіЃЌИљОнЯпЖЮДЙжБЦНЗжЯпЕФаджЪЁЂЯрЫЦШ§НЧаЮЕФаджЪМЦЫуЃЎ
НтЃКЃЈ1ЃЉШчЭМ1ЃЌ
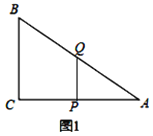
CP=AQ=tЃЌдђAP=8ЃtЃЌдкRtЁїABCжаЃЌгЩЙДЙЩЖЈРэПЩЕУAB=10ЃЌ
гЩPQЁЮCBПЩЕУ![]() ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ
НтЕУt=![]() ЃЌЫљвдЕБt=
ЃЌЫљвдЕБt=![]() ЪБЃЌPQЁЮCB .
ЪБЃЌPQЁЮCB .
ЃЈ2ЃЉДцдкЃЌШчЭМ2ЃЌ
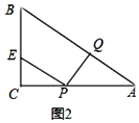
гЩЬтвтПЩжЊCP=AQ=tЃЌгжЁпЁЯPCE =90ЁуЃЌвЊЪЙЁїCEPгыЁїPQAШЋЕШЃЌ
жЛгаЁЯPQA=90ЁуЃЌ
етвЛжжЧщПіЃЌДЫЪБCE=PQЃЌPE= APЃЌгЩЁїPQAЁзЁїBCAПЩЕУ![]() ЃЌ
ЃЌ
МД![]() ЃЌНтЕУt=
ЃЌНтЕУt=![]() ЃЌ
ЃЌ
дђPE=8Ѓt=![]() ЃЌдкRtЁїPCEжаЃЌгЩЙДЙЩЖЈРэПЩЕУCE=
ЃЌдкRtЁїPCEжаЃЌгЩЙДЙЩЖЈРэПЩЕУCE=![]() ЃЛ
ЃЛ
(ЛђгЩЁїPCEЁзЁїACBЕУ![]() ЃЌМД
ЃЌМД![]() ЃЌНтЕУCE=
ЃЌНтЕУCE=![]() ЃЉ
ЃЉ
ЃЈ3ЃЉЂйЕБPгЩCЯђAдЫЖЏЪБЃЌCQ=CP=AQ=tЃЌПЩЕУЁЯQCA=ЁЯQACЃЌ
ЫљвдЁЯQCB=ЁЯQBCЃЌЫљвдCQ=BQ=tЃЌЫљвдBQ=AQ=![]() ABЃЌ
ABЃЌ
МДAB=2tЃЌНтЕУt=5ЃЛ
ЂкШчЭМ3ЃЌ
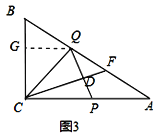
ЕБPгЩAЯђCдЫЖЏЪБЃЌЙ§QзїQGЁЭCBНЛCBгкЕуGЃЌ
CQ=CP=16ЃtЃЌBQ=10ЃtЃЌдђ![]() ЃЌМД
ЃЌМД![]() ЃЌЫљвдGQ=
ЃЌЫљвдGQ=![]() ЃЈ10ЃtЃЉЃЌ
ЃЈ10ЃtЃЉЃЌ
ЭЌРэПЩЧѓЕУBG=![]() ЃЈ10ЃtЃЉЃЌЫљвдGC=6Ѓ
ЃЈ10ЃtЃЉЃЌЫљвдGC=6Ѓ![]() ЃЈ10ЃtЃЉЃЌ
ЃЈ10ЃtЃЉЃЌ
дкRtЁїCGQжаЃЌгЩЙДЙЩЖЈРэПЩЕУЃКCG2+GQ2=CQ2ЃЌ
МД[6Љ![]() ЃЈ10ЃtЃЉ]2+[
ЃЈ10ЃtЃЉ]2+[![]() ЃЈ10ЃtЃЉ]2=ЃЈ16ЃtЃЉ2ЃЌНтЕУt=10.
ЃЈ10ЃtЃЉ]2=ЃЈ16ЃtЃЉ2ЃЌНтЕУt=10.
злЩЯПЩжЊТњзуЬѕМўЕФtЕФжЕЮЊ5КЭ10ЃЎ


 НђЧХНЬг§ЪюМйАЮИпЯЮНгЙуЖЋШЫУёГіАцЩчЯЕСаД№АИ
НђЧХНЬг§ЪюМйАЮИпЯЮНгЙуЖЋШЫУёГіАцЩчЯЕСаД№АИ ВЈВЈамЪюМйзївЕНЮїШЫУёГіАцЩчЯЕСаД№АИ
ВЈВЈамЪюМйзївЕНЮїШЫУёГіАцЩчЯЕСаД№АИ бЇЖјгХЪюЦкЯЮНгФЯОЉДѓбЇГіАцЩчЯЕСаД№АИ
бЇЖјгХЪюЦкЯЮНгФЯОЉДѓбЇГіАцЩчЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСагяОфжаЃЌВЛЪЧУќЬтЕФЮЊЃЈЁЁЁЁЃЉ
A. ЖдЖЅНЧЯрЕШ B. ЭЌвЛЦНУцФкЃЌСНЬѕжБЯпЛђепЯрНЛЃЌЛђепЦНаа
C. зїжБЯпl D. ЕШЪНЃЈxЉyЃЉ2=x2+xy+y2
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаЕШЪНГЩСЂЕФЪЧЃЈ ЃЉ
A. ЃЈ-a-bЃЉ2+ЃЈa-bЃЉ2=-4ab B. ЃЈ-a-bЃЉ2+ЃЈa-bЃЉ2=a2+b2
C. ЃЈ-a-bЃЉЃЈa-bЃЉ=ЃЈa-bЃЉ2 D. ЃЈ-a-bЃЉЃЈa-bЃЉ=b2-a2
ЁОД№АИЁПD
ЁОНтЮіЁПНтЮіЃКЁпЃЈ-a-bЃЉ2+ЃЈa-bЃЉ2=ЃЈa+bЃЉ2+ЃЈa-bЃЉ2=ЃЈa2+2ab+b2ЃЉ+ЃЈa2-2ab+b2ЃЉ=2a2+2b2ЃЌ
ЁрбЁЯюAгыбЁЯюBДэЮѓЃЛ
ЁпЃЈ-a-bЃЉЃЈa-bЃЉ=-ЃЈa+bЃЉЃЈa-bЃЉ=-ЃЈa2-b2ЃЉ=b2-a2ЃЌЁрбЁЯюCДэЮѓЃЌбЁЯюDе§ШЗ.
ЙЪбЁD.
ЁОЬтаЭЁПЕЅбЁЬт
ЁОНсЪјЁП
8
ЁОЬтФПЁПШєx=1ЃЌy=![]() ЃЌдђx2+4xy+4y2ЕФжЕЪЧЃЈ ЃЉ
ЃЌдђx2+4xy+4y2ЕФжЕЪЧЃЈ ЃЉ
A. 2 B. 4 C. 32 D. 12
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєx=1ЃЌy=![]() ЃЌдђx2+4xy+4y2ЕФжЕЪЧЃЈ ЃЉ
ЃЌдђx2+4xy+4y2ЕФжЕЪЧЃЈ ЃЉ
A. 2 B. 4 C. 32 D. 12
ЁОД№АИЁПB
ЁОНтЮіЁПНтЮіЃКx2+4xy+4y2=ЃЈx+2yЃЉ2=![]() =4.ЙЪбЁB.
=4.ЙЪбЁB.
ЁОЬтаЭЁПЕЅбЁЬт
ЁОНсЪјЁП
9
ЁОЬтФПЁПЯТСавђЪНЗжНтЃЌе§ШЗЕФЪЧЃЈ ЃЉ
A. x2y2-z2=x2ЃЈy+zЃЉЃЈy-zЃЉ B. -x2y+4xy-5y=-yЃЈx2+4x+5ЃЉ
C. ЃЈx+2ЃЉ2-9=ЃЈx+5ЃЉЃЈx-1ЃЉ D. 9-12a+4a2=-ЃЈ3-2aЃЉ2
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
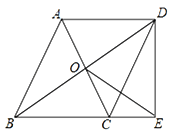
ЁОЬтФПЁПШчЭМЃЌЁѕABCDЕФЖдНЧЯпНЛгкЕуOЃЌЕуEдкБпBCЕФбгГЄЯпЩЯЃЌЧвOE=OBЃЌСЌНгDEЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїBDEЪЧжБНЧШ§НЧаЮЃЛ
ЃЈ2ЃЉШчЙћOEЁЭCDЃЌЪдХаЖЯЁїBDEгыЁїDCEЪЧЗёЯрЫЦЃЌВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯBAC=60ЁуЃЌBC=18ЃЌDЪЧABЩЯвЛЕуЃЌAC=BDЃЌEЪЧCDЕФжаЕу.дђAEЕФГЄЪЧ( ).
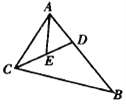
A. 12 B. 9 C. 9![]() D. вдЩЯЖМВЛЖд
D. вдЩЯЖМВЛЖд
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
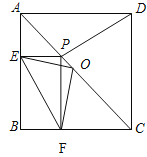
ЁОЬтФПЁПШчЭМЃЌвбжЊЃКдке§ЗНаЮABCDжаЃЌЕуPдкACЩЯЃЌPEЁЭABгкE,PFЁЭBCгкF.
ЃЈ1ЃЉЪдХаЖЯЯпЖЮEFгыPDЕФГЄЪЧЗёЯрЕШЃЌВЂЫЕУїРэгЩ.
ЃЈ2ЃЉШєЕуOЪЧACЕФжаЕуЃЌХаЖЯOFгыOEжЎМфгадѕбљЕФЮЛжУКЭЪ§СПЙиЯЕЃПВЂЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com