
【题目】如图,CB=CA,∠ACB=90°,点D在边BC上(与B,C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:①AC=FG;②S△FAB∶S四边形CBFG=1∶2;③∠ABC=∠ABF;④AD2=FQ·AC,其中正确结论的个数是( )

A. 1个 B. 2个 C. 3个 D. 4个
【答案】D
【解析】试题解析:∵四边形ADEF为正方形,
∴∠FAD=90°,AD=AF=EF,
∴∠CAD+∠FAG=90°,
∵FG⊥CA,
∴∠GAF+∠AFG=90°,
∴∠CAD=∠AFG,
在△FGA和△ACD中,
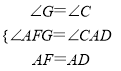 ,
,
∴△FGA≌△ACD(AAS),
∴AC=FG,①正确;
∵BC=AC,
∴FG=BC,
∵∠ACB=90°,FG⊥CA,
∴FG∥BC,
∴四边形CBFG是矩形,
∴∠CBF=90°,S△FAB=![]() FBFG=
FBFG=![]() S四边形CBFG,②正确;
S四边形CBFG,②正确;
∵CA=CB,∠C=∠CBF=90°,
∴∠ABC=∠ABF=45°,③正确;
∵∠FQE=∠DQB=∠ADC,∠E=∠C=90°,
∴△ACD∽△FEQ,
∴AC:AD=FE:FQ,
∴ADFE=AD2=FQAC,④正确;
故选D.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=60°,BC=18,D是AB上一点,AC=BD,E是CD的中点.则AE的长是( ).
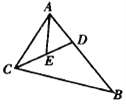
A. 12 B. 9 C. 9![]() D. 以上都不对
D. 以上都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
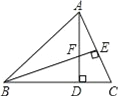
【题目】如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D,E,AD与BE相交于点F.
(1)求证:△ACD∽△BFD;
(2)当tan∠ABD=1.2,AC=3时,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
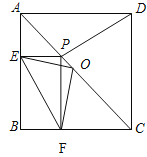
【题目】如图,已知:在正方形ABCD中,点P在AC上,PE⊥AB于E,PF⊥BC于F.
(1)试判断线段EF与PD的长是否相等,并说明理由.
(2)若点O是AC的中点,判断OF与OE之间有怎样的位置和数量关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AD=2AB,点F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF,CF,则下列结论中一定成立的是____.(把所有正确结论的序号都填在横线上)

①∠DCF=![]() ∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.
∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com