
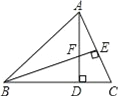
【题目】如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D,E,AD与BE相交于点F.
(1)求证:△ACD∽△BFD;
(2)当tan∠ABD=1.2,AC=3时,求BF的长.
【答案】(1)证明见解析;(2)BF=2.5.
【解析】试题分析:(1)由AD⊥BC,BE⊥AC,∠BDF=∠ADC=∠BEC=90°,从而得到∠DBF=∠DAC, 问题得证;
(2)由tan∠ABD=1.2,∠ADB=90°,可得AD与BD的比值,再由相似三角形的对应边的比相等,由(1)中的两三角形相似即可求得BF的值.
试题解析:(1)∵AD⊥BC,BE⊥AC,
∴∠BDF=∠ADC=∠BEC=90°,
∴∠C+∠DBF=90°,∠C+∠DAC=90°,
∴∠DBF=∠DAC,
∴△ACD∽△BFD.
(2)∵tan∠ABD=1,∠ADB=90°
∴![]() =1.2,
=1.2,
∵△ACD∽△BFD,
∴![]() =1.2,
=1.2,
∵AC=3
∴BF=2.5.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图1,在直角坐标系xoy中,O是坐标原点,点A在x正半轴上,OA=![]() cm,点B在y轴的正半轴上,OB=12cm,动点P从点O开始沿OA以
cm,点B在y轴的正半轴上,OB=12cm,动点P从点O开始沿OA以![]() cm/s的速度向点A移动,动点Q从点A开始沿AB以4cm/s的速度向点B移动,动点R从点B开始沿BO以2cm/s的速度向点O移动.如果P、Q、R分别从O、A、B同时移动,移动时间为t(0<t<6)s.
cm/s的速度向点A移动,动点Q从点A开始沿AB以4cm/s的速度向点B移动,动点R从点B开始沿BO以2cm/s的速度向点O移动.如果P、Q、R分别从O、A、B同时移动,移动时间为t(0<t<6)s.
(1)求∠OAB的度数.
(2)以OB为直径的⊙O′与AB交于点M,当t为何值时,PM与⊙O′相切?
(3)是否存在△RPQ为等腰三角形?若存在,请直接写出出的t值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>3b;(3)8a+7b+2c>0;(4)若点A(﹣3,y1)、点B(﹣![]() ,y2)、点C(
,y2)、点C(![]() ,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.
,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.
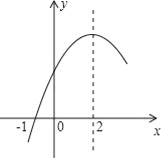
其中正确结论的序号是_______________.(在横线上填上你认为所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
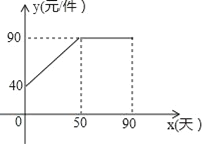
【题目】九年级某班数学兴趣小组经过市场调查整理出某种商品在第x天(1≤x≤90,且x为整数)的售价与销售量的相关信息如下.已知商品的进价为30元/件,设该商品的售价为y(单位:元/件),每天的销售量为p(单位:件),每天的销售利润为w(单位:元).
时间x(天) | 1 | 30 | 60 | 90 |
每天销售量p(件) | 198 | 140 | 80 | 20 |
(1)求出w与x的函数关系式;
(2)问销售该商品第几天时,当天的销售利润最大?并求出最大利润;
(3)该商品在销售过程中,共有多少天每天的销售利润不低于5600元?请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CB=CA,∠ACB=90°,点D在边BC上(与B,C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:①AC=FG;②S△FAB∶S四边形CBFG=1∶2;③∠ABC=∠ABF;④AD2=FQ·AC,其中正确结论的个数是( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某病毒细胞的直径约为0.000156cm,用科学记数法表示这个数是( )
A.0.156×10﹣3B.15.6×10﹣5C.1.56×10﹣4D.1.56×104
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为建设“美丽乡村”,需要对某村居民的自来水管进行改造,该工程若由甲队单独施工恰好在规定时间内完成;若由乙队单独施工,则完成工程所需时间是规定天数的1.5倍如果由甲、乙两队先合做10天,那么余下的工程由乙队单独完成还需5天.
(1)这项工程完成规定的时间是多少天?
(2)已知甲队每天的施工费用为6500元,乙队每天的施工费用为3600元,为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙两队合做来完成,则该工程施工费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平行四边形ABCD中,E,F是对角线BD上的两点, 如果添加一个条件使△ABE≌△CDF,则添加的条件不能是( )

A. AE=CF B. BE=FD C. BF=DE D. ∠1=∠2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com