
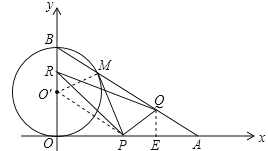
ЁОЬтФПЁПШчЭМ1ЃЌдкжБНЧзјБъЯЕxoyжаЃЌOЪЧзјБъдЕуЃЌЕуAдкxе§АыжсЩЯЃЌOAЃН![]() cmЃЌЕуBдкyжсЕФе§АыжсЩЯЃЌOBЃН12cmЃЌЖЏЕуPДгЕуOПЊЪМбиOAвд
cmЃЌЕуBдкyжсЕФе§АыжсЩЯЃЌOBЃН12cmЃЌЖЏЕуPДгЕуOПЊЪМбиOAвд![]() cm/sЕФЫйЖШЯђЕуAвЦЖЏЃЌЖЏЕуQДгЕуAПЊЪМбиABвд4cm/sЕФЫйЖШЯђЕуBвЦЖЏЃЌЖЏЕуRДгЕуBПЊЪМбиBOвд2cm/sЕФЫйЖШЯђЕуOвЦЖЏ.ШчЙћPЁЂQЁЂRЗжБ№ДгOЁЂAЁЂBЭЌЪБвЦЖЏЃЌвЦЖЏЪБМфЮЊtЃЈ0ЃМtЃМ6ЃЉs.
cm/sЕФЫйЖШЯђЕуAвЦЖЏЃЌЖЏЕуQДгЕуAПЊЪМбиABвд4cm/sЕФЫйЖШЯђЕуBвЦЖЏЃЌЖЏЕуRДгЕуBПЊЪМбиBOвд2cm/sЕФЫйЖШЯђЕуOвЦЖЏ.ШчЙћPЁЂQЁЂRЗжБ№ДгOЁЂAЁЂBЭЌЪБвЦЖЏЃЌвЦЖЏЪБМфЮЊtЃЈ0ЃМtЃМ6ЃЉs.
ЃЈ1ЃЉЧѓЁЯOABЕФЖШЪ§.
ЃЈ2ЃЉвдOBЮЊжБОЖЕФЁбOЁфгыABНЛгкЕуMЃЌЕБtЮЊКЮжЕЪБЃЌPMгыЁбOЁфЯрЧаЃП
ЃЈ3ЃЉЪЧЗёДцдкЁїRPQЮЊЕШбќШ§НЧаЮЃПШєДцдкЃЌЧыжБНгаДГіГіЕФtжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ

ЁОД№АИЁП(1) 30ЁуЃЎ(2) t=3ЪБЃЌPMгыЁбOЁЏЯрЧаЃЎ(3) t=8-2![]() ЃЌ
ЃЌ ![]() ЃЌ1+
ЃЌ1+![]() ЪБЃЌЁїRPQЮЊЕШбќШ§НЧаЮЃЎ
ЪБЃЌЁїRPQЮЊЕШбќШ§НЧаЮЃЎ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉдкRtЁїOABжаЃЌвбжЊСЫOAЁЂOBЕФГЄЃЌМДПЩЧѓГіЁЯOABЕФе§ЧажЕЃЌгЩДЫПЩЕУЕНЁЯOABЕФЖШЪ§ЃЛ
ЃЈ2ЃЉСЌНгOЁфMЃЌЕБPMгыЁбOЁфЯрЧаЪБЃЌPMЁЂPOЭЌЮЊЁбOЁфЕФЧаЯпЃЌвзжЄЕУЁїOOЁфPЁеЁїMOЁфPЃЌдђЁЯOOЁфP=ЁЯMOЁфPЃЛдкЃЈ1ЃЉжавзЕУЁЯOBA=60ЁуЃЌМДЁїOЁфBMЪЧЕШБпШ§НЧаЮЃЌгЩДЫПЩЕУЕНЁЯBOЁфM=ЁЯPOЁфM=ЁЯPOЁфO=60ЁуЃЛдкRtЁїOPOЁфжаЃЌИљОнЁЯPOЁфOЕФЖШЪ§МАOOЁфЕФГЄМДПЩЧѓЕУOPЕФГЄЃЌвбжЊСЫPЕуЕФдЫЖЏЫйЖШЃЌМДПЩИљОнЪБМф=ТЗГЬЁТЫйЖШЧѓЕУtЕФжЕЃЛ
ЃЈ3ЃЉДцдкЁїRPQЮЊЕШбќШ§НЧаЮЃЌгЩгкЁїQPQЕФбќКЭЕзВЛШЗЖЈЃЌашЗжРрЬжТлЃКЂйPR=RQЃЌЂкPR=PQЃЌЂлRQ=PQЪБЗжБ№ЧѓГіЗћКЯЬтвтЕФtжЕМДПЩЃЌ
ЪдЬтНтЮіЃКЃЈ1ЃЉдкRtЁїAOBжаЃК
tanЁЯOAB=![]() ЃЌ
ЃЌ
ЁрЁЯOAB=30ЁуЃЎ
ЃЈ2ЃЉШчЭМЃЌСЌНгOЁфPЃЌOЁфMЃЎ
ЕБPMгыЁбOЁфЯрЧаЪБЃЌгаЃК
ЁЯPMOЁф=ЁЯPOOЁф=90ЁуЃЌ
ЁїPMOЁфЁеЁїPOOЁфЃЎ
гЩЃЈ1ЃЉжЊЁЯOBA=60ЁуЃЌ
ЁпOЁфM=OЁфBЃЌ
ЁрЁїOЁфBMЪЧЕШБпШ§НЧаЮЃЌ
ЁрЁЯBOЁфM=60ЁуЃЎ
ПЩЕУЁЯOOЁфP=ЁЯMOЁфP=60ЁуЃЎ
ЁрOP=OOЁфtanЁЯOOЁфP
=6ЁСtan60Ёу=6![]() ЃЌ
ЃЌ
гжЁпOP=2![]() tЃЌ
tЃЌ
Ёр2![]() t=6
t=6![]() ЃЌ
ЃЌ
t=3ЃЎ
МДЃКt=3ЪБЃЌPMгыЁбOЁЏЯрЧаЃЎ
ЃЈ3ЃЉДцдкЁїRPQЮЊЕШбќШ§НЧаЮЃЌ
РэгЩШчЯТЃКгЩЬтвтПЩжЊЃКPR2=16t2-48tЃЌPQ2=52t2-288tЃЌRQ2=28t2-240t+576ЃЌ
ЕБЂйPR=RQЪБЃЌПЩЕУt=8-2![]() ЃЈt=8+
ЃЈt=8+![]() ЩсШЅЃЉЃЛ
ЩсШЅЃЉЃЛ
ЕБЂкPR=PQЪБЃЌПЩЕУt=![]() ЃЛ
ЃЛ
ЕБЂлRQ=PQЪБЃЌПЩЕУt=1+![]() ЃЈt=1-
ЃЈt=1-![]() ЩсШЅЃЉ
ЩсШЅЃЉ
злЩЯПЩжЊЃКЕБt=8-2![]() ЃЌ
ЃЌ ![]() ЃЌ1+
ЃЌ1+![]() ЪБЃЌЁїRPQЮЊЕШбќШ§НЧаЮЃЎ
ЪБЃЌЁїRPQЮЊЕШбќШ§НЧаЮЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєxmЁТx2n+1ЃНxЃЌдђmгыnЕФЙиЯЕЪЧЃЈ ЃЉ
A. mЃН2n+1 B. mЃНЉ2nЉ1 C. mЉ2nЃН2 D. mЉ2nЃНЉ2
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABЪЧАыдВOЕФжБОЖЃЌCЁЂDЪЧАыдВOЩЯЕФСНЕуЃЌЧвODЁЮBCЃЌODгыACНЛгкЕуEЃЎ

ЃЈ1ЃЉШєЁЯB=70ЁуЃЌЧѓЁЯCADЕФЖШЪ§ЃЛ
ЃЈ2ЃЉШєAB=4ЃЌAC=3ЃЌЧѓDEЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЭЌвЛЬѕЕРТЗЩЯЃЌМзГЕДгAЕиЕНBЕиЃЌввГЕДгBЕиЕНAЕиЃЌввЯШГіЗЂЃЌЭМжаЕФелЯпЖЮБэЪОМзЁЂввСНГЕжЎМфЕФОрРыyЃЈЧЇУзЃЉгыааЪЛЪБМфxЃЈаЁЪБЃЉЕФКЏЪ§ЙиЯЕЕФЭМЯѓЃЌЯТСаЫЕЗЈДэЮѓЕФЪЧЃЈЁЁЁЁЃЉ

A. ввЯШГіЗЂЕФЪБМфЮЊ0.5аЁЪБ B. МзЕФЫйЖШЪЧ80ЧЇУз/аЁЪБ
C. МзГіЗЂ0.5аЁЪБКѓСНГЕЯргі D. МзЕНBЕиБШввЕНAЕидч![]() аЁЪБ
аЁЪБ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊжБЯпy=kx+bОЙ§ЕуBЃЈ1ЃЌ4ЃЉЃЌЧвгыжБЯпy=-x-11ЦНааЃЎ
ЃЈ1ЃЉЧѓжБЯпABЕФНтЮіЪНВЂЧѓГіЕуCЕФзјБъЃЛ
ЃЈ2ЃЉИљОнЭМЯѓЃЌаДГіЙигкxЕФВЛЕШЪН0ЃМ2xЉ4ЃМkx+bЕФНтМЏЃЛ
ЃЈ3ЃЉЯжгавЛЕуPдкжБЯпABЩЯЃЌЙ§ЕуPзіPQЁЮyжсНЛжБЯпy=2x-4гкЕуQЃЌШєCЕуЕНЯпЖЮPQЕФОрРыЮЊ1ЃЌЧѓЕуPЕФзјБъВЂжБНгаДГіЯпЖЮPQЕФГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЖўДЮКЏЪ§y=ax2+bx+cЃЈaЁй0ЃЉЕФДѓжТЭМЯѓЃЌЙигкИУЖўДЮКЏЪ§ЯТСаЫЕЗЈе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ

A. aЃО0ЃЌbЃМ0ЃЌcЃО0
B. b2Љ4acЃМ0
C. ЕБЉ1ЃМxЃМ2ЪБЃЌyЃО0
D. ЕБx>2ЪБЃЌyЫцxЕФдіДѓЖјдіДѓ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєx=1ЃЌy=![]() ЃЌдђx2+4xy+4y2ЕФжЕЪЧЃЈ ЃЉ
ЃЌдђx2+4xy+4y2ЕФжЕЪЧЃЈ ЃЉ
A. 2 B. 4 C. 32 D. 12
ЁОД№АИЁПB
ЁОНтЮіЁПНтЮіЃКx2+4xy+4y2=ЃЈx+2yЃЉ2=![]() =4.ЙЪбЁB.
=4.ЙЪбЁB.
ЁОЬтаЭЁПЕЅбЁЬт
ЁОНсЪјЁП
9
ЁОЬтФПЁПЯТСавђЪНЗжНтЃЌе§ШЗЕФЪЧЃЈ ЃЉ
A. x2y2-z2=x2ЃЈy+zЃЉЃЈy-zЃЉ B. -x2y+4xy-5y=-yЃЈx2+4x+5ЃЉ
C. ЃЈx+2ЃЉ2-9=ЃЈx+5ЃЉЃЈx-1ЃЉ D. 9-12a+4a2=-ЃЈ3-2aЃЉ2
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
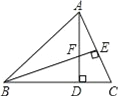
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌADЁЭBCЃЌBEЁЭACЃЌДЙзуЗжБ№ЮЊDЃЌEЃЌADгыBEЯрНЛгкЕуFЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїACDЁзЁїBFDЃЛ
ЃЈ2ЃЉЕБtanЁЯABD=1.2ЃЌAC=3ЪБЃЌЧѓBFЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com