
【题目】如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.

(1)若∠B=70°,求∠CAD的度数;
(2)若AB=4,AC=3,求DE的长.
【答案】(1)35°;(2)![]() .
.
【解析】试题分析:根据OD∥BC,∠DOA=∠B=70°,根据OA=OD可得∠DAO=∠ADO=55°,根据AB为直径可求出∠CAD的度数;根据Rt△ACB得出BC的长度,根据O为AB的中点,OD∥BC,从而得出OE和OD的长度,根据DE=OD-OE得出答案.
试题解析:(1)∵OD∥BC,∴∠DOA=∠B=70°. 又∵OA=OD,∴∠DAO=∠ADO=55°.
∵AB是直径,∴∠ACB=90°,∴∠CAB=20° ∴∠CAD=35°.
(2)在Rt△ACB中,BC=![]() . ∵圆心O是直径AB的中点,OD∥BC,
. ∵圆心O是直径AB的中点,OD∥BC,
∴OE=![]() BC=
BC=![]() 又OD=
又OD=![]() AB=2, ∴DE=OD-OE=2-
AB=2, ∴DE=OD-OE=2-![]()


科目:初中数学 来源: 题型:
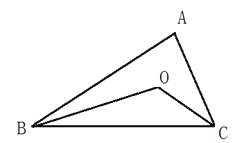
【题目】(本题共10分)AB和AC 相交于点A, BD和CD相交于点D,探究∠BDC与∠B 、 ∠C、∠BAC的关系.
小明是这样做的:
解:以点A为端点作射线AD.
∵∠1是△ABD的外角,∴∠1= ∠B+∠BAD.
同理∠2=∠C+∠CAD.
∴∠1+∠2=∠B+∠BAD+∠C+∠CAD.即∠BDC=∠B+∠C+∠BAC.
小英的思路是:延长BD交AC于点E.
(1)按小英的思路完成∠BDC=∠B+∠C+∠BAC这一结论.



(2)按照上面的思路解决如下问题:如图:在△ABC中,BE、CD分别是∠ABC∠ACB的角平分线,交AC于E,交AB于D.BE、CD相交于点O,∠A=60°.求∠BOC的度数.

(3)如图:△ABC中,BO、CO分别是∠ABC与∠ACB的角平分线,且BO、CO相交于点O.猜想∠BOC与∠A有怎样的关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,以AB为直径的⊙O分别与BC,AC相交于点D,E,BD=CD,过点D作⊙O的切线交边AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为5,∠CDF=30°,求![]() 的长(结果保留π).
的长(结果保留π).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中适合采用抽样调查的是( )
A.调查本班同学的身高情况B.飞机起飞前,对相关零部件进行检查
C.调查春节联欢晚会的收视率D.选出某班短跑跑得最快的学生参加学校比赛
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在直角坐标系xoy中,O是坐标原点,点A在x正半轴上,OA=![]() cm,点B在y轴的正半轴上,OB=12cm,动点P从点O开始沿OA以
cm,点B在y轴的正半轴上,OB=12cm,动点P从点O开始沿OA以![]() cm/s的速度向点A移动,动点Q从点A开始沿AB以4cm/s的速度向点B移动,动点R从点B开始沿BO以2cm/s的速度向点O移动.如果P、Q、R分别从O、A、B同时移动,移动时间为t(0<t<6)s.
cm/s的速度向点A移动,动点Q从点A开始沿AB以4cm/s的速度向点B移动,动点R从点B开始沿BO以2cm/s的速度向点O移动.如果P、Q、R分别从O、A、B同时移动,移动时间为t(0<t<6)s.
(1)求∠OAB的度数.
(2)以OB为直径的⊙O′与AB交于点M,当t为何值时,PM与⊙O′相切?
(3)是否存在△RPQ为等腰三角形?若存在,请直接写出出的t值;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com