
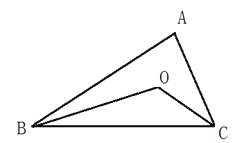
����Ŀ�������10�֣�AB��AC �ཻ�ڵ�A�� BD��CD�ཻ�ڵ�D��̽����BDC���B �� ��C����BAC�Ĺ�ϵ��
��������������
�����Ե�AΪ�˵�������AD��
�ߡ�1�ǡ�ABD����������1= ��B+��BAD��
ͬ����2=��C+��CAD��
���1+��2=��B+��BAD+��C+��CAD������BDC=��B+��C+��BAC��
СӢ��˼·�����ӳ�BD��AC�ڵ�E��
��1����СӢ��˼·��ɡ�BDC=��B+��C+��BAC��һ���ۣ�



��2�����������˼·���������������ͼ���ڡ�ABC����BE��CD�ֱ��ǡ�ABC��ACB�Ľ�ƽ��������AC��E����AB��D��BE��CD�ཻ�ڵ�O����A=60�������BOC�Ķ�����

��3����ͼ����ABC����BO��CO�ֱ��ǡ�ABC���ACB�Ľ�ƽ��������BO��CO�ཻ�ڵ�O�������BOC���A�������Ĺ�ϵ��������֤����
���𰸡���1��֤������������2��120������3����BOC=90��+ ![]() ��A��
��A��
�����������������
��1����СӢ��˼·����BDC�ǡ�DCE����ǣ���DEC�ǡ�ABE����ǣ�������������ǵ����ʿɵã���BDC=��C+��DEC����DEC=��B+��BAC���ɴ˿ɵã���BDC=��C+��B+��BAC��
��2������ABC����BE��CD�ֱ�����ABC��ACB�Ľ�ƽ��������AC��E����AB��D��BE��CD�ཻ�ڵ�O���ɵ���ABO+��ACO=![]() ����ABC+��ACB��=
����ABC+��ACB��=![]() ��180��-��A��=60����
��180��-��A��=60����
������1���ɵá�BOC=��ABO+��ACO+��A=120����
��3���ɣ�2���ɵã���ABO+��ACO=![]() ��180��-��A��=90��-
��180��-��A��=90��-![]() ��A�����ɣ�1���ɵã���BOC=��ABO+��ACO+��A=90��-
��A�����ɣ�1���ɵã���BOC=��ABO+��ACO+��A=90��-![]() ��A+��A=90��+
��A+��A=90��+![]() ��A.
��A.
���������
��1���ӳ�BD��AC��E��
�ߡ�BDC= ��C+��CED����CED=��BAC+��B��
���BDC=��C+��B+��BAC��
��2���ߡ�ABC����BE��CD�ֱ��ǡ�ABC��ACB�Ľ�ƽ������
���ABE=![]() ��ABC����ACD=
��ABC����ACD=![]() ��ACB��
��ACB��
���ABE+��ACD=![]() ����ABC+��ACB��=
����ABC+��ACB��=![]() ��180��-��A��=60����
��180��-��A��=60����
�ɣ�1��֪��BOC=��ABE+��ACD+��A
���BOC=60��+60��=120����
��3����BOC����A�Ĺ�ϵ����BOC=90��+![]() ��A������������
��A������������
�ߡ�ABC����BO��CO�ֱ��ǡ�ABC��ACB�Ľ�ƽ������
���ABO=![]() ��ABC����ACO=
��ABC����ACO=![]() ��ACB��
��ACB��
���ABO+��ACO=![]() ����ABC+��ACB��=
����ABC+��ACB��=��180��-��A��=90��-
![]() ��A��
��A��
��������1����֪����BOC=��ABO+��ACO+��A��
���BOC=90��-![]() ��A+��A=90��+
��A+��A=90��+![]() ��A.
��A.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ֱ��y=��3���У�x�����������ǣ� ��
A.һ��������
B.һ��������
C.����������
D.����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ���ǣ�������
A.�߶�AB���߶�BA��ʾ�IJ���ͬһ���߶�B.x2y��ϵ����1��������2
C.����ʽ4x2y��2xy+1�Ĵ�����3D.����AB������BA��ʾ����ͬһ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC��Rt��DEF������C=90������F=90����BC=EF����������һ��������_____________________��ʹ��ABC�ա�DEF��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������㣬�������Ǵ�����ǣ� ��
A.a4��a3=a7B.a6��a3=a3C.(a3)2=a5D.a3��b3=(a��b)3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�ķ���![]()
��1����֤������![]() ȡ�κ�ʵ��ʱ�����̺���ʵ������
ȡ�κ�ʵ��ʱ�����̺���ʵ������
��2��������![]() �Ķ��κ���
�Ķ��κ���![]() ��ͼ����
��ͼ����![]() ����������ĺ������Ϊ��������m������ֵ.
����������ĺ������Ϊ��������m������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����xm��x2n+1��x����m��n�Ĺ�ϵ�ǣ� ��
A. m��2n+1 B. m����2n��1 C. m��2n��2 D. m��2n����2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǰ�ԲO��ֱ����C��D�ǰ�ԲO�ϵ����㣬��OD��BC��OD��AC���ڵ�E��

��1������B=70��������CAD�Ķ�����
��2����AB=4��AC=3����DE�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com