
【题目】如图:在Rt△ABC和Rt△DEF中,∠C=90°,∠F=90°,BC=EF.请你添加一个条件:_____________________,使△ABC≌△DEF.

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
【题目】对于二次函数![]() 和一次函数
和一次函数![]() ,把
,把![]()
![]() 称为这两个函数的“再生二次函数”,其中t是不为零的实数,其图象记作抛物线L.现有点A(2,0)和抛物线L上的点B(﹣1,n),请完成下列任务:
称为这两个函数的“再生二次函数”,其中t是不为零的实数,其图象记作抛物线L.现有点A(2,0)和抛物线L上的点B(﹣1,n),请完成下列任务:
【尝试】(1)当t=2时,抛物线![]()
![]() 的顶点坐标为 ;
的顶点坐标为 ;
(2)判断点A (填是或否)在抛物线L上;
(3)n的值是 ;
【发现】通过(2)和(3)的演算可知,对于t取任何不为零的实数,抛物线L总过定点,坐标为 .
【应用】二次函数![]() 是二次函数
是二次函数![]() 和一次函数
和一次函数![]() 的一个“再生二次函数”吗?如果是,求出t的值;如果不是,说明理由.
的一个“再生二次函数”吗?如果是,求出t的值;如果不是,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图点D、E分别在等边ΔABC边BC、CA上,且CD=AE,联结AD、 BE.
(1)求证:BE=AD;
(2)延长DA交BE于F,求∠BFD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题共10分)AB和AC 相交于点A, BD和CD相交于点D,探究∠BDC与∠B 、 ∠C、∠BAC的关系.
小明是这样做的:
解:以点A为端点作射线AD.
∵∠1是△ABD的外角,∴∠1= ∠B+∠BAD.
同理∠2=∠C+∠CAD.
∴∠1+∠2=∠B+∠BAD+∠C+∠CAD.即∠BDC=∠B+∠C+∠BAC.
小英的思路是:延长BD交AC于点E.
(1)按小英的思路完成∠BDC=∠B+∠C+∠BAC这一结论.



(2)按照上面的思路解决如下问题:如图:在△ABC中,BE、CD分别是∠ABC∠ACB的角平分线,交AC于E,交AB于D.BE、CD相交于点O,∠A=60°.求∠BOC的度数.

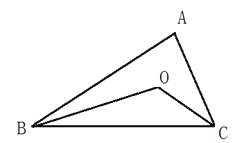
(3)如图:△ABC中,BO、CO分别是∠ABC与∠ACB的角平分线,且BO、CO相交于点O.猜想∠BOC与∠A有怎样的关系,并加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com