
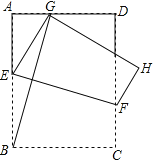
【题目】如图,将矩形![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在
落在![]() 边上的点
边上的点![]() 处,点
处,点![]() 落在点
落在点![]() 处,已知
处,已知![]() ,连接
,连接![]() ,则
,则![]() __________.
__________.
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,已知点![]() 在反比例函数
在反比例函数![]() 的图象上,过点
的图象上,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,直线
,直线![]() 经过点
经过点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,且
,且![]() ,
,![]() .
.

(1)求反比例函数![]() 和一次函数
和一次函数![]() 的表达式;
的表达式;
(2)直接写出关于![]() 的不等式
的不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料并完成任务:
点![]() 在数轴上分别表示有理数
在数轴上分别表示有理数![]() ;
;![]() 两点之间的距离表示为
两点之间的距离表示为![]() .
.
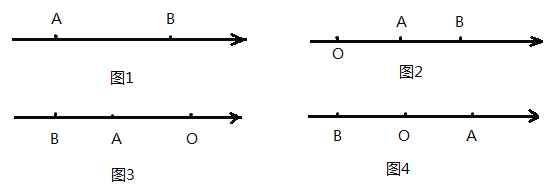
当![]() 两点中有一点在原点时,不妨设点
两点中有一点在原点时,不妨设点![]() 在原点,如图1所示,
在原点,如图1所示, ![]() ;
;
当![]() 两点都不在原点时,分三种情况,
两点都不在原点时,分三种情况,
情况一:如图2所示,点![]() 都在原点的右侧,
都在原点的右侧,![]() ;
;
情况二:如图3所示,点![]() 都在原点左侧,
都在原点左侧,![]() ;
;
情况三:如图4所示,点![]() 在原点的两边,
在原点的两边,![]() ;
;
综上所述,若点![]() 在数轴上分别表示有理数
在数轴上分别表示有理数![]() ,则数轴上
,则数轴上![]() 两点之间的距离为
两点之间的距离为![]() .
.
任务一:数轴上表示2和5的两点之间的距离是________,数轴上表示-2和-5的两点之间的距离是________,数轴上表示3和-1的两点之间的距离是________.
任务二:点![]() 在数轴上分别表示有理数
在数轴上分别表示有理数![]() ,那么
,那么![]() 到
到![]() 的距离与
的距离与![]() 到
到![]() 的距离之和可表示为_________(用含绝对值的式子表示).如果
的距离之和可表示为_________(用含绝对值的式子表示).如果![]() ,那么
,那么![]() 为________.
为________.
任务三:当![]() 取最小值时,
取最小值时, ![]() =________,
=________, ![]() =________.
=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O为坐标原点,点A(8,0)动点P从A出发以每秒2个单位长度的速度沿线段AO向终点O运动,同时动点Q从O出发以相同速度沿y轴正半轴运动,点P到达点O,两点同时停止运动.
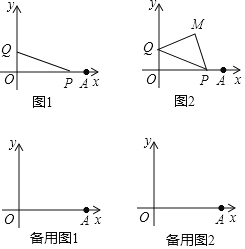
(1)当t= 时,∠OPQ=45°;
(2)如图2,以PQ为斜边在第一象限作等腰Rt△PQM,求M点坐标;
(3)在(2)的条件下,点R位x轴负半轴上一点,且![]() ,点M关于PQ的对称点为N,求t为何值时,△ONR为等腰直角三角形;
,点M关于PQ的对称点为N,求t为何值时,△ONR为等腰直角三角形;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MON=90°,OB=4,点A是直线OM上的一个动点,连结AB,作∠MAB与∠ABN的角平分线AF与BF,两条角平分线所在的直线相交于点F,则点A在运动过程中线段BF的最小值为( )
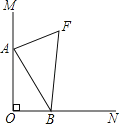
A. 4B. ![]() C. 8D. 2
C. 8D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
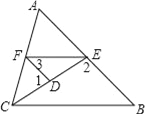
【题目】如图,已知∠1,∠2互为补角,且∠3=∠B,
(1)求证:∠AFE=∠ACB
(2)若CE平分∠ACB,且∠1=80°,∠3=45°,求∠AFE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
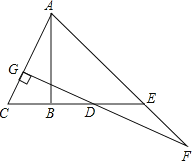
【题目】如图,AB垂直平分线段CD(AB>CD),点E是线段CD延长线上的一点,且BE=AB,连接AC,过点D作DG⊥AC于点G,交AE的延长线与点F.
(1)若∠CAB=α,则∠AFG= (用α的代数式表示);
(2)线段AC与线段DF相等吗?为什么?
(3)若CD=6,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】建设中的大外环路是我市的一项重点民生工程.某工程公司承建的一段路基工程的施工土方量为120万立方,原计划由公司的甲、乙两个工程队从公路的两端同时相向施工150天完成.由于特殊情况需要,公司抽调甲队外援施工,由乙队先单独施工40天后甲队返回,两队又共同施工了110天,这时甲乙两队共完成土方量103.2万立方.
(1)问甲、乙两队原计划平均每天的施工土方量分别为多少万立方?
(2)在抽调甲队外援施工的情况下,为了保证150天完成任务,公司为乙队新购进了一批机械来提高效率,那么乙队平均每天的施工土方量至少要比原来提高多少万立方才能保证按时完成任务?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com