
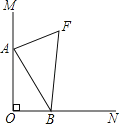
【题目】如图,∠MON=90°,OB=4,点A是直线OM上的一个动点,连结AB,作∠MAB与∠ABN的角平分线AF与BF,两条角平分线所在的直线相交于点F,则点A在运动过程中线段BF的最小值为( )
A. 4B. ![]() C. 8D. 2
C. 8D. 2![]()
【答案】D
【解析】
分情况讨论:当点A在射线OM上时,过F作FE⊥ON于E,FH⊥OM于H,FG⊥AB于G,由角平分线的性质得出FH=FG,FG=FE,得出FH=FE,证出点F在∠MON的角平分线上;当点A在射线OM的反向延长线上时,同理得出点F在∠MON的角平分线上;当BF⊥OF时,BF取最小值,证出△BOF是等腰直角三角形,即可得出答案.
解:当点A在射线OM上时,过F作FE⊥ON于E,FH⊥OM于H,FG⊥AB于G,
如图1所示:
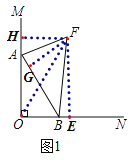
∵AF与BF分别是∠MAB与∠ABN的角平分线,
∴FH=FG,FG=FE,
∴FH=FE,
∴点F在∠MON的角平分线上;
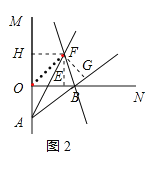
当点A在射线OM的反向延长线上时,过F作FE⊥ON于E,FH⊥OM于H,FG⊥AB交AB的延长线于G,
如图2所示:
∵AF与BF分别是∠MAB与∠ABN的角平分线,
∴FH=FG,FG=FE,
∴FH=FE,
∴点F在∠MON的角平分线上;
综上所述,点F在∠MON的角平分线上,
∴当BF⊥OF时,BF取最小值,
∵∠MON=90°,OB=4,
∴∠FON=![]() ∠MON=45°,
∠MON=45°,
∴△BOF是等腰直角三角形,
∴BF=![]() OB=2
OB=2![]() ;
;
故选:D.


科目:初中数学 来源: 题型:
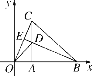
【题目】如图,在平面直角坐标系中,等腰△OBC的边OB在x轴上,OB=CB,OB边上的高CA与OC边上的高BE相交于点D,连接OD,AB=![]() ,∠CBO=45°,在直线BE上求点M,使△BMC与△ODC相似,则点M的坐标是________.
,∠CBO=45°,在直线BE上求点M,使△BMC与△ODC相似,则点M的坐标是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
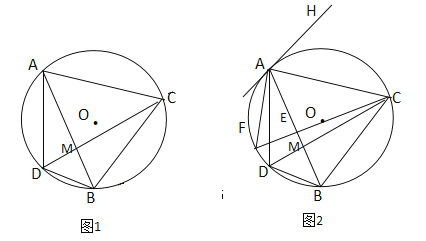
【题目】如图1,已知⊙O是ΔADB的外接圆,∠ADB的平分线DC交AB于点M,交⊙O于点C,连接AC,BC.
(1)求证:AC=BC;
(2)如图2,在图1 的基础上做⊙O的直径CF交AB于点E,连接AF,过点A作⊙O的切线AH,若AH//BC,求∠ACF的度数;
(3)在(2)的条件下,若ΔABD的面积为![]() ,ΔABD与ΔABC的面积比为2:9,求CD的长.
,ΔABD与ΔABC的面积比为2:9,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
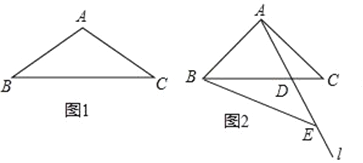
【题目】钝角三角形ABC中,∠BAC>90°,AB=AC,∠ACB=α,过点A的直线l交BC边于点D.点E在直线l上,且BC=BE.,点E在AD延长线上.
①当α=30°,点D恰好为BC中点时,补全图1直接写出∠BAE= °,
∠BEA= °;
②如图2,若∠BAE=2α,求∠BEA的度数(用含α的代数式表示);
查看答案和解析>>
科目:初中数学 来源: 题型:
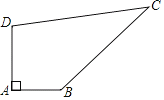
【题目】如图,某开发区有一块四边形的空地ABCD,现计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,则要投入_____元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数的图像过点![]() ,
,![]() ,与
,与![]() 轴交于另一点
轴交于另一点![]() ,且对称轴是直线
,且对称轴是直线![]() .
.
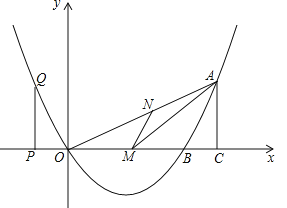
(1)求该二次函数的解析式;
(2)若![]() 是
是![]() 上的一点,作
上的一点,作![]() 交
交![]() 于
于![]() ,当
,当![]() 面积最大时,求
面积最大时,求![]() 的坐标;
的坐标;
(3)![]() 是
是![]() 轴上的点,过
轴上的点,过![]() 作
作![]() 轴,与抛物线交于
轴,与抛物线交于![]() ,过
,过![]() 作
作![]() 轴于
轴于![]() .当以
.当以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 、
、![]() 、
、![]() 为顶点的三角形相似时,求
为顶点的三角形相似时,求![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
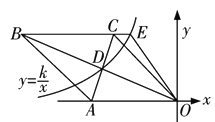
【题目】如图,菱形OABC的一边OA在x轴的负半轴上,O是坐标原点,A点坐标为(-10,0),对角线AC和OB相交于点D且AC·OB=160.若反比例函数y=![]() (x<0)的图象经过点D,并与BC的延长线交于点E,则S△OCE∶S△OAB=________.
(x<0)的图象经过点D,并与BC的延长线交于点E,则S△OCE∶S△OAB=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
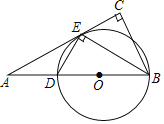
【题目】如图,在Rt△ABC中,∠C=90°,BE平分∠ABC交AC于点E,作ED⊥EB交AB于点D,⊙O是△BED的外接圆.
(1)求证:AC是⊙O的切线;
(2)已知⊙O的半径为2.5,BE=4,求BC,AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com