
【题目】如图,已知二次函数的图像过点![]() ,
,![]() ,与
,与![]() 轴交于另一点
轴交于另一点![]() ,且对称轴是直线
,且对称轴是直线![]() .
.
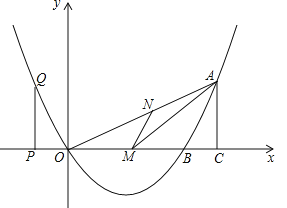
(1)求该二次函数的解析式;
(2)若![]() 是
是![]() 上的一点,作
上的一点,作![]() 交
交![]() 于
于![]() ,当
,当![]() 面积最大时,求
面积最大时,求![]() 的坐标;
的坐标;
(3)![]() 是
是![]() 轴上的点,过
轴上的点,过![]() 作
作![]() 轴,与抛物线交于
轴,与抛物线交于![]() ,过
,过![]() 作
作![]() 轴于
轴于![]() .当以
.当以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 、
、![]() 、
、![]() 为顶点的三角形相似时,求
为顶点的三角形相似时,求![]() 点的坐标.
点的坐标.
【答案】(1)y=![]() x2﹣
x2﹣![]() x;(2)当t=3时,S△AMN有最大值3,此时M点坐标为(3,0);(3)P点坐标为(14,28)或(﹣2,4)或(2,﹣1).
x;(2)当t=3时,S△AMN有最大值3,此时M点坐标为(3,0);(3)P点坐标为(14,28)或(﹣2,4)或(2,﹣1).
【解析】(1)先利用抛物线的对称性确定B(6,0),然后设交点式求抛物线解析式;
(2)设M(t,0),先其求出直线OA的解析式为y=![]() x,直线AB的解析式为y=2x﹣12,直线MN的解析式为y=2x﹣2t,再通过解方程组
x,直线AB的解析式为y=2x﹣12,直线MN的解析式为y=2x﹣2t,再通过解方程组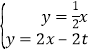 得N(
得N(![]() t,
t,![]() t),接着利用三角形面积公式,利用S△AMN=S△AOM﹣S△NOM得到S△AMN=
t),接着利用三角形面积公式,利用S△AMN=S△AOM﹣S△NOM得到S△AMN=![]() 4t﹣
4t﹣![]() t
t![]() t,然后根据二次函数的性质解决问题;
t,然后根据二次函数的性质解决问题;
(3)设Q(m,![]() m2﹣
m2﹣![]() m),根据相似三角形的判定方法,当
m),根据相似三角形的判定方法,当![]() =
=![]() 时,△PQO∽△COA,则|
时,△PQO∽△COA,则|![]() m2﹣
m2﹣![]() m|=2|m|;当
m|=2|m|;当![]() =
=![]() 时,△PQO∽△CAO,则|
时,△PQO∽△CAO,则|![]() m2﹣
m2﹣![]() m|=
m|=![]() |m|,然后分别解关于m的绝对值方程可得到对应的P点坐标.
|m|,然后分别解关于m的绝对值方程可得到对应的P点坐标.
(1)∵抛物线过原点,对称轴是直线x=3,
∴B点坐标为(6,0),
设抛物线解析式为y=ax(x﹣6),
把A(8,4)代入得a82=4,解得a=![]() ,
,
∴抛物线解析式为y=![]() x(x﹣6),即y=
x(x﹣6),即y=![]() x2﹣
x2﹣![]() x;
x;
(2)设M(t,0),
易得直线OA的解析式为y=![]() x,
x,
设直线AB的解析式为y=kx+b,
把B(6,0),A(8,4)代入得![]() ,解得
,解得![]() ,
,
∴直线AB的解析式为y=2x﹣12,
∵MN∥AB,
∴设直线MN的解析式为y=2x+n,
把M(t,0)代入得2t+n=0,解得n=﹣2t,
∴直线MN的解析式为y=2x﹣2t,
解方程组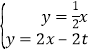 得
得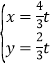 ,则N(
,则N(![]() t,
t,![]() t),
t),
∴S△AMN=S△AOM﹣S△NOM
=![]() 4t﹣
4t﹣![]() t
t![]() t
t
=﹣![]() t2+2t
t2+2t
=﹣![]() (t﹣3)2+3,
(t﹣3)2+3,
当t=3时,S△AMN有最大值3,此时M点坐标为(3,0);
(3)设Q(m,![]() m2﹣
m2﹣![]() m),
m),
∵∠OPQ=∠ACO,
∴当![]() =
=![]() 时,△PQO∽△COA,即
时,△PQO∽△COA,即![]() =
=![]() ,
,
∴PQ=2PO,即|![]() m2﹣
m2﹣![]() m|=2|m|,
m|=2|m|,
解方程![]() m2﹣
m2﹣![]() m=2m得m1=0(舍去),m2=14,此时P点坐标为(14,28);
m=2m得m1=0(舍去),m2=14,此时P点坐标为(14,28);
解方程![]() m2﹣
m2﹣![]() m=﹣2m得m1=0(舍去),m2=﹣2,此时P点坐标为(﹣2,4);
m=﹣2m得m1=0(舍去),m2=﹣2,此时P点坐标为(﹣2,4);
∴当![]() =
=![]() 时,△PQO∽△CAO,即
时,△PQO∽△CAO,即![]() =
=![]() ,
,
∴PQ=![]() PO,即|
PO,即|![]() m2﹣
m2﹣![]() m|=
m|=![]() |m|,
|m|,
解方程![]() m2﹣
m2﹣![]() m=
m=![]() m得m1=0(舍去),m2=8(舍去),
m得m1=0(舍去),m2=8(舍去),
解方程![]() m2﹣
m2﹣![]() m=﹣
m=﹣![]() m得m1=0(舍去),m2=2,此时P点坐标为(2,﹣1);
m得m1=0(舍去),m2=2,此时P点坐标为(2,﹣1);
综上所述,P点坐标为(14,28)或(﹣2,4)或(2,﹣1).


科目:初中数学 来源: 题型:
【题目】如图,在边长为a的正方形的一角剪去一个边长为b的正方形,把剩余的部分(图中的阴影部分)裁剪后拼成右边的长方形.
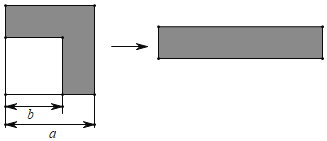
(1)请写出上述剪拼过程中所揭示的乘法公式;
(2)请运用乘法公式简便计算:20192﹣2020×2018.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MON=90°,OB=4,点A是直线OM上的一个动点,连结AB,作∠MAB与∠ABN的角平分线AF与BF,两条角平分线所在的直线相交于点F,则点A在运动过程中线段BF的最小值为( )
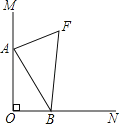
A. 4B. ![]() C. 8D. 2
C. 8D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
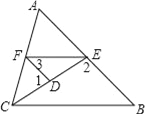
【题目】如图,已知∠1,∠2互为补角,且∠3=∠B,
(1)求证:∠AFE=∠ACB
(2)若CE平分∠ACB,且∠1=80°,∠3=45°,求∠AFE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某自行车厂计划一周生产自行车1400辆,平均每天生产200辆,但由于种种原因,实际每天生产量与计划量相比有出入,下表是某周的生产情况(超产记为正、减产记为负):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 七 |
增减产值 |
|
|
|
|
|
|
|
(1)根据记录的数据可知该厂星期五生产自行车__________辆.
(2)根据记录的数据可知该厂本周实际生产自行车_________辆.
(3)该厂实行每日计件工资制,每生产一辆车可得60元,若超额完成任务,则超过部分每辆另奖15元,若没有完成任务,少生产一辆扣20元,那么该厂工人这一周的工作总额是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
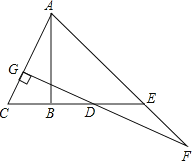
【题目】如图,AB垂直平分线段CD(AB>CD),点E是线段CD延长线上的一点,且BE=AB,连接AC,过点D作DG⊥AC于点G,交AE的延长线与点F.
(1)若∠CAB=α,则∠AFG= (用α的代数式表示);
(2)线段AC与线段DF相等吗?为什么?
(3)若CD=6,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是我县新区部分小区位置简图.设港澳城为点A,水榭花都为点B,朝阳家园为点C,滨海华庭为点D,阳光家园为点E,盛世嘉苑为点F,设每个小格的单位为1.
(1)请建立适当的平面直角坐标系,并写出六个小区的坐标;
(2)依次连接点A、C、E、B,请求出四边形ACEB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
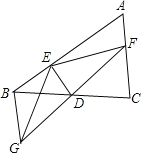
【题目】如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.
(1)求证:BG=CF;
(2)请你判断BE+CF与EF的大小关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com