练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如果为互不相等的有理数，且，那么（ ）

    A.8B.6C.4D.2

    【答案】B

    【解析】

    根据已知条件确定a，b，c，d之间的关系，然后利用|a-c|=|b-c|=|d-b|=2得出|a-d|的值．

    解：已知b≠c，可设b＜c，

    ∵|a-c|=|b-c|，

    ∴a-c与b-c必互为相反数（否则a=b，不合题意），即a-c=-(b-c)，

    ∴a+b=2c，

    又∵b＜c，

    ∴a＞c．

    ∵|b-c|=|d-b|，

    ∴b-c与d-b必相等（否则c=d，不合题意），即b-c=d-b，

    ∴2b=c+d，

    ∵b＜c，

    ∴b＞d，

    即d＜b＜c＜a．

    ∴|a-d|=a-d=(a-c)+(c-b)+(b-d)=2+2+2=6．

    若设b＞c，同理可得|a-d|=6．

    故选B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系xOy中，已知点M，N的坐标分别为（﹣1，2），（2，1），若抛物线y=ax2﹣x+2（a≠0）与线段MN有两个不同的交点，则a的取值范围是（　　）

    A. a≤﹣1或≤a＜ B. ≤a＜

    C. a≤或a＞ D. a≤﹣1或a≥

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某地电话拨号入网有两种收费方式,用户可以任选其一.

    计时制:0.05元/分;

    包月制:50元/月(限一部个人住宅电话上网).

    此外,每一种上网方式都得加收通信费0.02元/分.

    (1)某用户某月上网的时间为x小时,请你分别写出两种收费方式下该用户应该支付的费用.

    (2)若某用户估计一个月内上网的时间为20小时,你认为采用哪种方式较为合算?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

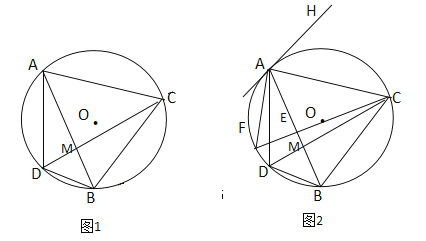
    【题目】如图1，已知⊙O是ΔADB的外接圆，∠ADB的平分线DC交AB于点M，交⊙O于点C，连接AC，BC.

    （1）求证：AC=BC；

    （2）如图2，在图1 的基础上做⊙O的直径CF交AB于点E，连接AF，过点A作⊙O的切线AH，若AH//BC，求∠ACF的度数；

    （3）在（2）的条件下，若ΔABD的面积为，ΔABD与ΔABC的面积比为2：9，求CD的长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】随着我国网络信息技术的不断发展，在课堂中恰当使用信息技术辅助教学是时代提出的新要求，阳谷县为了解初中数学老师对“网络画板”信息技术的掌握情况，对部分初中数学老师进行了调查，并根据调查结果绘制成如下不完整的统计图表．

    掌握情况

    非常熟练

    比较熟练

    不太熟练

    基本不会

    人数

    20

    16

    请根据图表信息，解答下列问题：

    （1）求表中的值；

    （2）求图中表示“比较熟练”的扇形部分的圆心角的度数；

    （3）阳谷县共有初中数学教师350人，若将“非常熟练”和“比较熟练”作为“良好”标准，试估计阳谷县初中数学教师对“网络画板”信息技术掌握情况为“良好”的教师有多少人？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

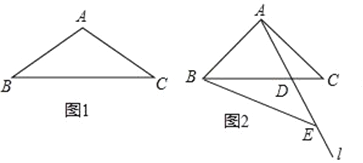
    【题目】钝角三角形ABC中，∠BAC＞90°，AB=AC，∠ACB=α，过点A的直线l交BC边于点D．点E在直线l上，且BC=BE．，点E在AD延长线上．

    ①当α=30°，点D恰好为BC中点时，补全图1直接写出∠BAE=　°，

    ∠BEA=　°；

    ②如图2，若∠BAE=2α，求∠BEA的度数（用含α的代数式表示）；

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，将矩形沿折叠，使点落在边上的点处，点落在点处，已知，连接，则__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知二次函数的图像过点,,与轴交于另一点,且对称轴是直线.

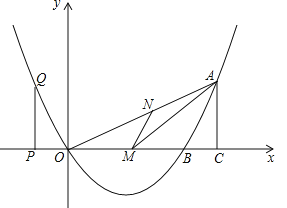
    （1）求该二次函数的解析式；

    （2）若是上的一点，作交于,当面积最大时，求的坐标；

    （3）是轴上的点，过作轴，与抛物线交于,过作轴于.当以、、为顶点的三角形与、、为顶点的三角形相似时，求点的坐标.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

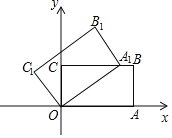
    【题目】如图，在平面直角坐标系中，矩形OABC的两边OA，OC分别在x轴和y轴上，并且OA=5，OC=3．若把矩形OABC绕着点O逆时针旋转，使点A恰好落在BC边上的A1处，则点C的对应点C1的坐标为（　　）

    A. （﹣） B. （﹣） C. （﹣） D. （﹣）

    查看答案和解析>>

    同步练习册答案