
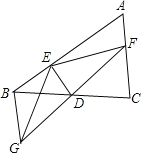
【题目】如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.
(1)求证:BG=CF;
(2)请你判断BE+CF与EF的大小关系,并说明理由.
【答案】(1)详见解析;(2)BE+CF>EF,证明详见解析
【解析】
(1)先利用ASA判定△BGD![]() CFD,从而得出BG=CF;
CFD,从而得出BG=CF;
(2)利用全等的性质可得GD=FD,再有DE⊥GF,从而得到EG=EF,两边之和大于第三边从而得出BE+CF>EF.
解:(1)∵BG∥AC,
∴∠DBG=∠DCF.
∵D为BC的中点,
∴BD=CD
又∵∠BDG=∠CDF,
在△BGD与△CFD中,
∵
∴△BGD≌△CFD(ASA).
∴BG=CF.
(2)BE+CF>EF.
∵△BGD≌△CFD,
∴GD=FD,BG=CF.
又∵DE⊥FG,
∴EG=EF(垂直平分线到线段端点的距离相等).
∴在△EBG中,BE+BG>EG,
即BE+CF>EF.


科目:初中数学 来源: 题型:
【题目】如图,已知二次函数的图像过点![]() ,
,![]() ,与
,与![]() 轴交于另一点
轴交于另一点![]() ,且对称轴是直线
,且对称轴是直线![]() .
.
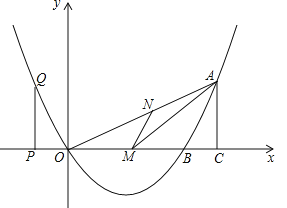
(1)求该二次函数的解析式;
(2)若![]() 是
是![]() 上的一点,作
上的一点,作![]() 交
交![]() 于
于![]() ,当
,当![]() 面积最大时,求
面积最大时,求![]() 的坐标;
的坐标;
(3)![]() 是
是![]() 轴上的点,过
轴上的点,过![]() 作
作![]() 轴,与抛物线交于
轴,与抛物线交于![]() ,过
,过![]() 作
作![]() 轴于
轴于![]() .当以
.当以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 、
、![]() 、
、![]() 为顶点的三角形相似时,求
为顶点的三角形相似时,求![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
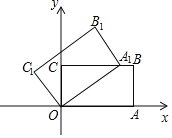
【题目】如图,在平面直角坐标系中,矩形OABC的两边OA,OC分别在x轴和y轴上,并且OA=5,OC=3.若把矩形OABC绕着点O逆时针旋转,使点A恰好落在BC边上的A1处,则点C的对应点C1的坐标为( )
A. (﹣![]() ) B. (﹣
) B. (﹣![]() ) C. (﹣
) C. (﹣![]() ) D. (﹣
) D. (﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
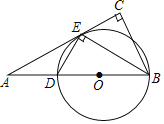
【题目】如图,在Rt△ABC中,∠C=90°,BE平分∠ABC交AC于点E,作ED⊥EB交AB于点D,⊙O是△BED的外接圆.
(1)求证:AC是⊙O的切线;
(2)已知⊙O的半径为2.5,BE=4,求BC,AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:用分离系数法进行整式的加减运算.
我们已经学过整式的加减,而我们可以列竖式进行整式的加减运算,只要将参加运算的整式连同字母进行降幂排列,凡缺项则留出空位或添零,然后让常数项对齐(即右对齐)即可.例如,计算(x3﹣2x2﹣5)﹣(x﹣2x2﹣1)时,我们可以用下列竖式计算:
竖式:
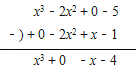
(x3﹣2x2+5)﹣(x﹣2x2﹣1)=x3﹣x﹣4
这种方法叫做分离系数法.用分离系数法计算:
(1)(2x2+4x﹣3)+(5﹣4x+x2);
(2)(3y3﹣5y2﹣6)﹣(y﹣2+3y3).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,O是AC上一动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.若点O运动到AC的中点,则∠ACB=_____°时,四边形AECF是正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
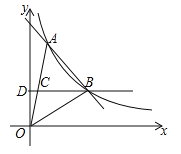
【题目】(2017山东省菏泽市,第20题,7分)如图,一次函数y=kx+b与反比例函数![]() 的图象在第一象限交于A、B两点,B点的坐标为(3,2),连接OA、OB,过B作BD⊥y轴,垂足为D,交OA于C,若OC=CA.
的图象在第一象限交于A、B两点,B点的坐标为(3,2),连接OA、OB,过B作BD⊥y轴,垂足为D,交OA于C,若OC=CA.
(1)求一次函数和反比例函数的表达式;
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y1=﹣x2+4x和直线y2=2x.我们规定:当x取任意一个值时,x对应的函数值分别为y1和y2,若y1≠y2,取y1和y2中较小值为M;若y1=y2,记M=y1=y2.①当x>2时,M=y2;②当x<0时,M随x的增大而增大;③使得M大于4的x的值不存在;④若M=2,则x=1.上述结论正确的是_____(填写所有正确结论的序号).
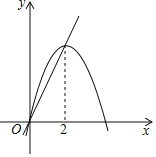
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用对称性可设计出美丽的图案.在边长为1的方格纸中,有如图所示的四边形(顶点都在格点上).
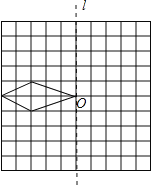
(1)先作出该四边形关于直线![]() 成轴对称的图形,再作出你所作的图形连同原四边形绕0点按顺时针方向旋转90o后的图形;
成轴对称的图形,再作出你所作的图形连同原四边形绕0点按顺时针方向旋转90o后的图形;
(2)完成上述设计后,整个图案的面积等于_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com