
【题目】如图,已知抛物线y1=﹣x2+4x和直线y2=2x.我们规定:当x取任意一个值时,x对应的函数值分别为y1和y2,若y1≠y2,取y1和y2中较小值为M;若y1=y2,记M=y1=y2.①当x>2时,M=y2;②当x<0时,M随x的增大而增大;③使得M大于4的x的值不存在;④若M=2,则x=1.上述结论正确的是_____(填写所有正确结论的序号).
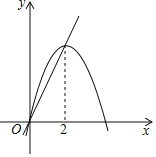
【答案】②③
【解析】①观察函数图象,可知:当x>2时,抛物线y1=-x2+4x在直线y2=2x的下方,进而可得出当x>2时,M=y1,结论①错误;
②观察函数图象,可知:当x<0时,抛物线y1=-x2+4x在直线y2=2x的下方,进而可得出当x<0时,M=y1,再利用二次函数的性质可得出M随x的增大而增大,结论②正确;
③利用配方法可找出抛物线y1=-x2+4x的最大值,由此可得出:使得M大于4的x的值不存在,结论③正确;
④利用一次函数图象上点的坐标特征及二次函数图象上点的坐标特征求出当M=2时的x值,由此可得出:若M=2,则x=1或2+![]() ,结论④错误.
,结论④错误.
此题得解.
①当x>2时,抛物线y1=-x2+4x在直线y2=2x的下方,
∴当x>2时,M=y1,结论①错误;
②当x<0时,抛物线y1=-x2+4x在直线y2=2x的下方,
∴当x<0时,M=y1,
∴M随x的增大而增大,结论②正确;
③∵y1=-x2+4x=-(x-2)2+4,
∴M的最大值为4,
∴使得M大于4的x的值不存在,结论③正确;
④当M=y1=2时,有-x2+4x=2,
解得:x1=2-![]() (舍去),x2=2+
(舍去),x2=2+![]() ;
;
当M=y2=2时,有2x=2,
解得:x=1.
∴若M=2,则x=1或2+![]() ,结论④错误.
,结论④错误.
综上所述:正确的结论有②③.
故答案为:②③.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图是我县新区部分小区位置简图.设港澳城为点A,水榭花都为点B,朝阳家园为点C,滨海华庭为点D,阳光家园为点E,盛世嘉苑为点F,设每个小格的单位为1.
(1)请建立适当的平面直角坐标系,并写出六个小区的坐标;
(2)依次连接点A、C、E、B,请求出四边形ACEB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
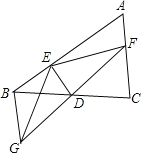
【题目】如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.
(1)求证:BG=CF;
(2)请你判断BE+CF与EF的大小关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图是由一些火柴棒搭成的图案:
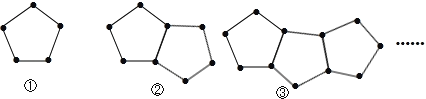
(1)摆第①个图案用 根火柴棒,摆第②个图案用 根火柴棒,摆第③个图案用 根火柴棒.
(2)按照这种方式摆下去,摆第n个图案用多少根火柴棒?
(3)计算一下摆121根火柴棒时,是第几个图案?
查看答案和解析>>
科目:初中数学 来源: 题型:
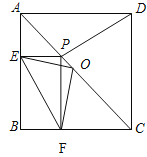
【题目】如图,已知:在正方形ABCD中,点P在AC上,PE⊥AB于E,PF⊥BC于F.
(1)试判断线段EF与PD的长是否相等,并说明理由.
(2)若点O是AC的中点,判断OF与OE之间有怎样的位置和数量关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是等边三角形,D为边AC的中点,AE⊥EC,BD=EC.
(1)求证:△BDA≌△CEA;
(2)请判断△ADE是什么三角形,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】多项式4x2+1加上一个单项式,使它成为一个整式的完全平方,则这个单项式可以是__________________.(填写符合条件的一个即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,对四边形ABCD是平行四边形的下列判断,正确的打“√”,错误的打“×”.
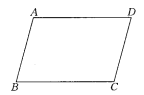
(1)因为AD∥BC,AB=CD,所以ABCD是平行四边形.(____)
(2)因为AB∥CD,AD=BC,所以ABCD是平行四边形.(____)
(3)因为AD∥BC,AD=BC,所以ABCD是平行四边形.(____)
(4)因为AB∥CD,AD∥BC,所以ABCD是平行四边形.(____)
(5)因为AB=CD,AD=BC,所以ABCD是平行四边形.(____)
(6)因为AD=CD,AB=AC,所以ABCD是平行四边形.(____)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com