
【题目】如图,已知△ABC是等边三角形,D为边AC的中点,AE⊥EC,BD=EC.
(1)求证:△BDA≌△CEA;
(2)请判断△ADE是什么三角形,并说明理由.

【答案】(1)见解析;(2)见解析.
【解析】
(1)易证∠ADB=∠AEC=90°,AB=AC,即可证明Rt△BDA≌Rt△CEA,即可解题;
(2)根据(1)中结论可得AE=CD,根据直角三角形斜边的中线等于斜边的一半的性质可得AD=DE,即可解题.
证明:(1)∵△ABC是等边三角形,
∴AB=BC=AC,
∵D是AC中点,
∴∠CBD=∠ABD=30°,∠BDA=90°,
∵AE⊥EC,
∴∠AEC=90°,
在Rt△BDA和Rt△CEA中,
![]() ,
,
∴Rt△BDA≌Rt△CEA(HL);
(2)∵△BDA≌△CEA,
∴AE=AD,
∵D为边AC的中点,AE⊥EC,
∴AD=DE,
∴AD=DE=AE,
∴△ADE是等边三角形.


科目:初中数学 来源: 题型:
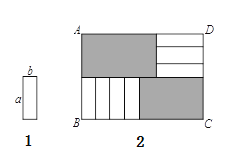
【题目】7张如图的长为![]() ,宽为
,宽为![]() 的小长方形纸片,按如图的方式不重叠地放在矩形
的小长方形纸片,按如图的方式不重叠地放在矩形![]() 内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为
内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为![]() ,当
,当![]() 的长度变化时,则
的长度变化时,则![]() ,
,![]() 满足( )
满足( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线l经过点A,BD⊥直线l,CE⊥直线l,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线l上,且∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立;请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是直线l上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,求证:DF=EF.

查看答案和解析>>
科目:初中数学 来源: 题型:
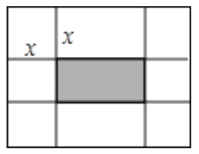
【题目】在槐荫区初中数学文化年的开幕式上,同学们为我们展示了研究性学习“怎样制作一个尽可能大的无盖长方体盒子”.现在有一个长是60cm,宽为40cm的长方形硬纸片做成一个无盖的长方体盒子,于是在长方形的四个角各剪去一个相同的小正方形(如图).
(1)若设这些小正方形的边长为x cm,求图中阴影部分的面积.
(2)当x-5时,求这个盒子的体积
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点A顺时针旋转60°得到△ADE,点C的对应点E恰好落在BA的延长线上,DE与BC交于点F,连接BD.下列结论不一定正确的是( )
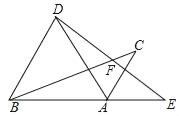
A. AD=BD B. AC∥BD C. DF=EF D. ∠CBD=∠E
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,CE平分∠ACD,AE平分∠BAC,∠EAC+∠ACE=90°
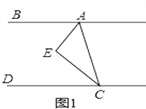
(1)请判断AB与CD的位置关系并说明理由;
(2)如图2,在(1)的结论下,当∠E=90°保持不变,移动直角顶点E,使∠MCE=∠ECD,当直角顶点E点移动时,问∠BAE与∠MCD是否存在确定的数量关系?

(3)如图3,在(1)的结论下,P为线段AC上一定点,点Q为直线CD上一动点,当点Q在射线CD上运动时(点C除外)∠CPQ+∠CQP与∠BAC有何数量关系? (2、3小题只需选一题说明理由)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com