
【题目】解下列方程组:
(1)![]() ;
;
(2)![]() ;
;
(3) 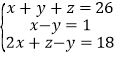 .
.
【答案】(1) ![]() ,(2)
,(2) ![]() ;(3)
;(3)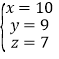 .
.
【解析】
(1)用代入消元法解二元一次方程组可得答案;
(2)用加减消元法解二元一次方程组可得答案;
(3)用消元法解三元一次方程组可得答案.
(1)将方程x-5y=2变形,得x=2+5y.
把x=2+5y代入方程3x+2y=-11,
得3(2+5y)+2y=-11,解得y=-1.
把y=-1代入x=2+5y,得x=-3.所以原方程组的解是![]() ’
’
(2)![]()
①+②,得4x=12,解得x=3.
将x=3代入①,得3+2y=1,解得y=-1.所以原方程组的解是![]() .
.
(3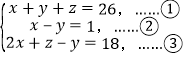
由②,得x=y+1,④
把④代入①,得2y+z=25,⑤
把④代入③,得y+z=16,⑥
⑤与⑥组成方程组![]() ,
,
解这个方程组,得![]() ,
,
把y=9代入④,得x=9+1=10.
所以原方程组的解为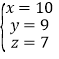 .
.


科目:初中数学 来源: 题型:
【题目】完成下面的证明
如图,FG//CD,∠1=∠3,∠B=50°,求∠BDE的度数.

解:∵FG//CD (已知)
∴∠2=_________(____________________________)
又∵∠1=∠3,
∴∠3=∠2(等量代换)
∴BC//__________(_____________________________)
∴∠B+________=180°(______________________________)
又∵∠B=50°
∴∠BDE=________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读与思考:
阅读理解问题——代数问题几何化 1.阅读理解以下文字: 我们知道,多项式的因式分解就是将一个多项式化成几个整 式的积的形式.通过因式分解,我们常常将一个次数比较高 的多项式转化成几个次数较低的整式的积,来达到降次化简 的目的.这个思想可以引领我们解决很多相对复杂的代数问 题.
例如:方程 2x2+3x=0 就可以这样来解:
解:原方程可化为 x(2x+3)=0,
所以x=0 或者 2x+3=0.
解方程 2x+3=0,得 x=-![]() . ∴原方程的解为 x=0或x=-
. ∴原方程的解为 x=0或x=-![]() .
.
根据你的理解,结合所学知识,解决以下问题:
(1)解方程:3x2-x=0
(2)解方程:(x+3)2-4x2=0;
(3)已知△ABC 的三边长为 4,x,y,请你判断代数式y2 -8y+16-x2的值的符号.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ACB中,∠ACB=90°,∠ABC的平分线BE和∠BAC的外角平分线AD相交于点P,分别交AC和BC的延长线于E,D.过P作PF⊥AD交AC的延长线于点H,交BC的延长线于点F,连接AF交DH于点G.则下列结论:①∠APB=45°;②PF=PA;③BD﹣AH=AB;④DG=AP+GH.其中正确的是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,在四边形ABCD中,AB∥DC,E是BC的中点,若AE是∠BAD的平分线,求证:AD=DC+AB,
(2)如图②,在四边形ABCD中,AB∥DC,F是DC延长线上一点,连接AF,E是BC的中点,若AE是∠BAF的平分线,求证:AB=AF+CF.
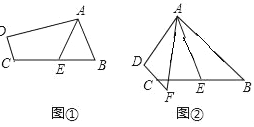
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:对于形如![]() 这样的二次三项式,可以用公式法将它分解成
这样的二次三项式,可以用公式法将它分解成![]() 的形式.但对于二次三项式
的形式.但对于二次三项式![]() ,就不能直接运用公式了.此时,我们可以在二次三项式
,就不能直接运用公式了.此时,我们可以在二次三项式![]() 中先加上一项
中先加上一项![]() ,使它与
,使它与![]() 的和成为一个完全平方式,再减去
的和成为一个完全平方式,再减去![]() ,整个式子的值不变,于是有:
,整个式子的值不变,于是有:![]()
![]()
![]()
![]()
像这样,先添一适当项,使式中出现完全平方式,再减去这个项,使整个式子的值不变的方法称为“配方法”,利用“配方法",解决下列问题:
(1)分解因式:![]() .
.
(2)比较代数式![]() 与
与![]() 的大小.
的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,点P是三角形内的任意一点,PD∥AB,PE∥BC,PF∥AC,若△ABC的周长为36,则PD+PE+PF=( )
A.12
B.8
C.4
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是等边三角形,D为边AC的中点,AE⊥EC,BD=EC.
(1)求证:△BDA≌△CEA;
(2)请判断△ADE是什么三角形,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com