
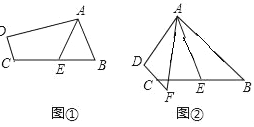
【题目】(1)如图①,在四边形ABCD中,AB∥DC,E是BC的中点,若AE是∠BAD的平分线,求证:AD=DC+AB,
(2)如图②,在四边形ABCD中,AB∥DC,F是DC延长线上一点,连接AF,E是BC的中点,若AE是∠BAF的平分线,求证:AB=AF+CF.
【答案】(1)证明见解析; (2)证明见解析.
【解析】
(1)延长AE交DC的延长线于点F,证明△AEB≌△FEC,根据全等三角形的性质得到AB=FC,根据等腰三角形的判定得到DF=AD,证明结论;
(2)延长AE交DF的延长线于点G,利用同(1)相同的方法证明.
解:(1)延长AE交DC的延长线于点F,
∵E是BC的中点,
∴CE=BE,
∵AB∥DC,
∴∠BAE=∠F,
在△AEB和△FEC中,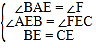 ,
,
∴△AEB≌△FEC,
∴AB=FC,
∵AE是∠BAD的平分线,
∴∠BAE=∠EAD,
∵AB∥CD,
∴∠BAE=∠F,
∴∠EAD=∠F,
∴AD=DF,
∴AD=DF=DC+CF=DC+AB,
(2)如图②,延长AE交DF的延长线于点G,
∵E是BC的中点,
∴CE=BE,
∵AB∥DC,
∴∠BAE=∠G,
在△AEB和△GEC中,  ,
,
∴△AEB≌△GEC,
∴AB=GC,
∵AE是∠BAF的平分线,
∴∠BAG=∠FAG,
∵AB∥CD,
∴∠BAG=∠G,
∴∠FAG=∠G,
∴FA=FG,
∴AB=CG=AF+CF.


科目:初中数学 来源: 题型:
【题目】阅读材料: 小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:![]() ,善于思考的小明进行了以下探索:
,善于思考的小明进行了以下探索:
设![]() (其中
(其中![]() 均为整数),则有
均为整数),则有![]() .
.
∴![]() .这样小明就找到了一种把部分
.这样小明就找到了一种把部分![]() 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
当![]() 均为正整数时,若
均为正整数时,若![]() ,用含m、n的式子分别表示
,用含m、n的式子分别表示![]() ,得
,得![]() = ,
= ,![]() = ;
= ;
(2)利用所探索的结论,找一组正整数![]() ,填空: + =( +
,填空: + =( + ![]() )2;
)2;
(3)若![]() ,且
,且![]() 均为正整数,求
均为正整数,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
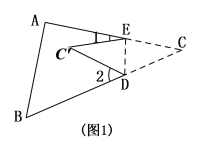
【题目】如图1,将△ABC纸片沿DE折叠,使点C落在四边形ABDE内点C’的位置,
(1)①若![]() ,则
,则![]() ;
;
②若![]() ,则
,则![]() ;
;
③探索![]() 、
、![]() 与
与![]() 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;
(2)直接按照所得结论,填空:
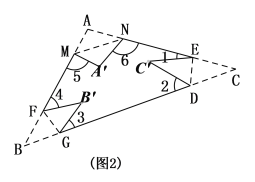
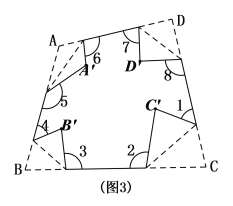
①如图中,将△ABC纸片再沿FG、MN折叠,使点A、B分别落在△ABC内点A’、B’的位置,则![]() ;
;
②如图中,将四边形ABCD按照上面方式折叠,则![]() ;
;
③若将n边形![]() 也按照上面方式折叠,则
也按照上面方式折叠,则![]() ;
;
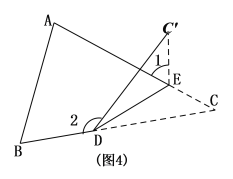
(3)如图,将△ABC纸片沿DE折叠,使点![]() 落在△ABC边
落在△ABC边![]() 上方点
上方点![]() 的位置, 探索
的位置, 探索![]() 、
、![]() 与
与![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
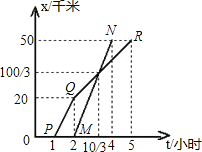
【题目】如图,AB两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也于同日下午骑摩托车从A地出发驶往B地,图中PQR和线段MN,分别表示甲和乙所行驶的S与该日下午时间t之间的关系,试根据图形回答:
(1)甲出发几小时,乙才开始出发?
(2)乙行驶多少分钟赶上甲,这时两人离B地还有多少千米?
(3)甲从下午2时到5时的速度是多少?
(4)乙行驶的速度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一架长25米的梯子,斜靠在竖直的墙上,这时梯子底端离墙7米.
(1)此时梯子顶端离地面多少米?
(2)若梯子顶端下滑4米,那么梯子底端将向左滑动多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国边防局接到情报,近海处有一可疑船只![]() 正向公海方向航行,边防部迅速派出快艇
正向公海方向航行,边防部迅速派出快艇![]() 追赶如图1,图2中
追赶如图1,图2中![]() 分别表示两船相对海岸的距离
分别表示两船相对海岸的距离![]() (海里)与追赶时间
(海里)与追赶时间![]() (分)之间的关系.
(分)之间的关系.

根据图象回答问题:
(1)哪条线表示![]() 到海岸的距离与追赶时间之间的关系?
到海岸的距离与追赶时间之间的关系?
(2)![]() 哪个速度快?
哪个速度快?
(3)15分钟内![]() 能否追上
能否追上![]() ?为什么?
?为什么?
(4)如果一直追下去,那么![]() 能否追上
能否追上![]() ?
?
(5)当![]() 逃离海岸12海里时,
逃离海岸12海里时,![]() 将无法对其进行检查,照此速度,
将无法对其进行检查,照此速度,![]() 能否在
能否在![]() 逃入公海前将其拦截?为什么?
逃入公海前将其拦截?为什么?
(6)![]() 与
与![]() 对应的两个一次函数
对应的两个一次函数![]() 与
与![]() 中,
中,![]() 的实际意义各是什么?可疑船只
的实际意义各是什么?可疑船只![]() 与快艇
与快艇![]() 的速度各是多少?
的速度各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD中,AE平分∠BAD,交BC于E,DE⊥AE,下列结论::①DE平分∠ADC;②E是BC的中点;③AD=2CD;④梯形ADCE的面积与△ABE的面积比是3:1,其中正确的结论的个数有( )
A.4
B.3
C.2
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线l经过点A,BD⊥直线l,CE⊥直线l,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线l上,且∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立;请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是直线l上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,求证:DF=EF.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com