
【题目】如图,AB两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也于同日下午骑摩托车从A地出发驶往B地,图中PQR和线段MN,分别表示甲和乙所行驶的S与该日下午时间t之间的关系,试根据图形回答:
(1)甲出发几小时,乙才开始出发?
(2)乙行驶多少分钟赶上甲,这时两人离B地还有多少千米?
(3)甲从下午2时到5时的速度是多少?
(4)乙行驶的速度是多少?
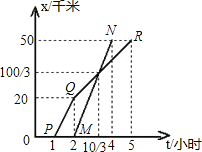
【答案】(1)甲下午1时出发,乙下午2时出发,甲出发1小时,乙才开始出发;(2)80分钟,![]() 千米;(3)10千米/时;(4)乙行驶的速度是25千米/时.
千米;(3)10千米/时;(4)乙行驶的速度是25千米/时.
【解析】
(1)由图可知,甲下午1时出发,乙下午2时出发;
(2)根据图像交点处的时间和距离,计算即可;
(3)时间为3小时,路程为30千米,从而得出速度;
(4)乙从A地到B地所用时间为2小时,再由速度、路程、时间之间的关系式求得答案.
解:(1)由图得:甲下午1时出发,乙下午2时出发,甲出发1小时,乙才开始出发;
(2)![]() 分钟,
分钟,![]() 千米,
千米,
乙行驶80分钟赶上甲,这时两人离B地还有![]() 千米.
千米.
(3)(50-20)÷(5-2)=10千米/时,甲从下午2时到5时的速度是10千米/时;
(4)50÷2=25千米/时,乙行驶的速度是25千米/时.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
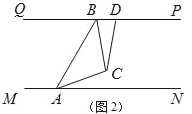
【题目】“一带一路”让中国和世界更紧密,“中欧铁路”为了安全起见在某段铁路两旁安置了两座可旋转探照灯.如图1所示,灯A射线从AM开始顺时针旋转至AN便立即回转,灯B射线从BP开始顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是每秒2度,灯B转动的速度是每秒1度.假定主道路是平行的,即PQ∥MN,且∠BAM:∠BAN=2:1.
(1)填空:∠BAN=_____°;
(2)若灯B射线先转动30秒,灯A射线才开始转动,在灯B射线到达BQ之前,A灯转动几秒,两灯的光束互相平行?
(3)如图2,若两灯同时转动,在灯A射线到达AN之前.若射出的光束交于点C,过C作∠ACD交PQ于点D,且∠ACD=120°,则在转动过程中,请探究∠BAC与∠BCD的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
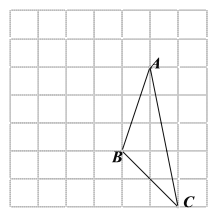
【题目】画图(只能借助于网格)并填空:
如图,每个小正方形的边长为![]() 个单位,每个小正方形的顶点叫格点.
个单位,每个小正方形的顶点叫格点.
(1)将![]() 向左平移
向左平移![]() 格,再向上平移
格,再向上平移![]() 格,请在图中画出平移后的
格,请在图中画出平移后的![]() ;
;
(2)![]() 的面积为 ;
的面积为 ;
(3)利用网格在图中画出△ABC的中线![]() ,高线
,高线![]() ;
;
(4)在图中能使![]() 的格点
的格点![]() 的个数有 个(点
的个数有 个(点![]() 异于
异于![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,一次函数的图象经过点A(2,3)与点B(0,5).
(1)求此一次函数的表达式;
(2)若点P为此一次函数图象上一点,且△POB的面积为10,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读与思考:
阅读理解问题——代数问题几何化 1.阅读理解以下文字: 我们知道,多项式的因式分解就是将一个多项式化成几个整 式的积的形式.通过因式分解,我们常常将一个次数比较高 的多项式转化成几个次数较低的整式的积,来达到降次化简 的目的.这个思想可以引领我们解决很多相对复杂的代数问 题.
例如:方程 2x2+3x=0 就可以这样来解:
解:原方程可化为 x(2x+3)=0,
所以x=0 或者 2x+3=0.
解方程 2x+3=0,得 x=-![]() . ∴原方程的解为 x=0或x=-
. ∴原方程的解为 x=0或x=-![]() .
.
根据你的理解,结合所学知识,解决以下问题:
(1)解方程:3x2-x=0
(2)解方程:(x+3)2-4x2=0;
(3)已知△ABC 的三边长为 4,x,y,请你判断代数式y2 -8y+16-x2的值的符号.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(a,b),B(c,0),|a-3|+(2b-c)2+![]() =0.
=0.

(1)求点A,B的坐标;
(2)如图,点C为x轴正半轴上一点,且OC=OA,点D为OC的中点,连AC,AD,请探索AD+CD与![]() AC之间的大小关系,并说明理由;
AC之间的大小关系,并说明理由;

(3)如图,过点A作AE⊥y轴于E,F为x轴负半轴上一动点( 不与(-3,0)重合 ),G在EF延长线上,以EG为一边作∠GEN=45°,过A作AM⊥x轴,交EN于点M,连FM,当点F在x轴负半轴上移动时,式子![]() 的值是否发生变化?若变化,求出变化的范围;若不变化,请求出其值并说明理由.
的值是否发生变化?若变化,求出变化的范围;若不变化,请求出其值并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,在四边形ABCD中,AB∥DC,E是BC的中点,若AE是∠BAD的平分线,求证:AD=DC+AB,
(2)如图②,在四边形ABCD中,AB∥DC,F是DC延长线上一点,连接AF,E是BC的中点,若AE是∠BAF的平分线,求证:AB=AF+CF.
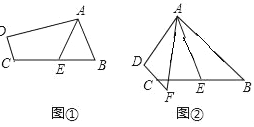
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了创建书香校园,今年又购进一批图书,经了解,科普书的单价比文学书的单价多4元,用1200元购进的科普书与用800元购进的文学书本数相等.
(1)今年购进的文学书和科普书的单价各是多少元?
(2)该校购买这两种书共180本,总费用不超过2000元,且购买文学书的数量不多于42本,应选择哪种购买方案可使总费用最低?最低费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC的度数是( )
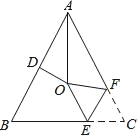
A. 106°B. 108°C. 110°D. 112°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com