
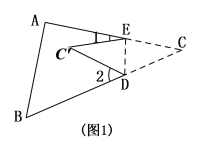
【题目】如图1,将△ABC纸片沿DE折叠,使点C落在四边形ABDE内点C’的位置,
(1)①若![]() ,则
,则![]() ;
;
②若![]() ,则
,则![]() ;
;
③探索![]() 、
、![]() 与
与![]() 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;
(2)直接按照所得结论,填空:
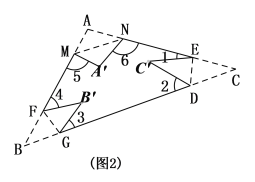
①如图中,将△ABC纸片再沿FG、MN折叠,使点A、B分别落在△ABC内点A’、B’的位置,则![]() ;
;
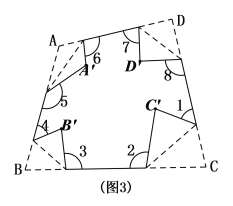
②如图中,将四边形ABCD按照上面方式折叠,则![]() ;
;
③若将n边形![]() 也按照上面方式折叠,则
也按照上面方式折叠,则![]() ;
;
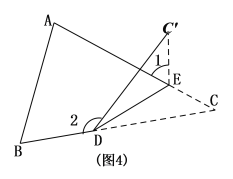
(3)如图,将△ABC纸片沿DE折叠,使点![]() 落在△ABC边
落在△ABC边![]() 上方点
上方点![]() 的位置, 探索
的位置, 探索![]() 、
、![]() 与
与![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
【答案】(1)①![]() ;②
;②![]() ;③
;③![]() ;(2)①
;(2)①![]() ;②
;②![]() ;③
;③![]() ;(3)
;(3)![]()
【解析】
(1)①由邻补角的定义可知∠CEC′=160°,∠CDC′=130°,根据折叠的性质可求出∠CED=80°,∠CDE=65°,然后根据三角形内角和定理求解即可;
②由三角形内角和可求出∠CED+∠CDE=138°,再由折叠的性质可知∠CEC′+∠CDC′=276°,然后根据邻补角的定义可求出![]() 84°;
84°;
③由邻补角定义可知![]() ,从而
,从而![]() ,所以,∠1+ ∠CEC′+ ∠2+ ∠CDC′=360 °,结合
,所以,∠1+ ∠CEC′+ ∠2+ ∠CDC′=360 °,结合![]() ,可求出
,可求出![]() ;
;
(2)① 由(1)得![]() 2∠C,
2∠C,![]() 2∠B,
2∠B,![]() 2∠A,从而
2∠A,从而![]() 2(∠A+∠B +∠C),结合三角形内角和求解即可;
2(∠A+∠B +∠C),结合三角形内角和求解即可;
②由①可知,![]() 2(∠A+∠B +∠C+∠D),结合四边形内角和求解即可;
2(∠A+∠B +∠C+∠D),结合四边形内角和求解即可;
③由①可知,![]() ;
;
(3)由外角的性质可知∠2=∠3+∠C,∠3=∠1+∠C,整理可得![]() .
.
解:(1)①∵![]() ,
,
∴∠CEC′=160°,∠CDC′=130°,
∵ ∠CED=80°,∠CDE=65°,
∴∠C= 180°-80°-65°=35°;
②∵
∴ ∠CED+∠CDE=180°-42°=138°,
∴∠CEC′+∠CDC′=276°,
∴![]() 360°-276°=84°;
360°-276°=84°;
③![]() ,
,
因为![]() ,
,![]() ,
,
所以![]() ,
,
因为在四边形![]() 中,
中,![]() ,
,
所以![]() ,
,
因为![]() ,
,
所以![]() .
.
(2)① 由①得
![]() 2∠C,
2∠C,![]() 2∠B,
2∠B,![]() 2∠A,
2∠A,
∴![]() 2(∠A+∠B +∠C)=360°;
2(∠A+∠B +∠C)=360°;
②∵![]() 2∠C,
2∠C,![]() 2∠B,
2∠B,![]() 2∠A,
2∠A,![]() 2∠D,
2∠D,
∴![]() 2(∠A+∠B +∠C+∠D)=2×360°=720°;
2(∠A+∠B +∠C+∠D)=2×360°=720°;
③∵n边形内角和是![]() ,
,
∴![]() ;
;
(3)![]() .
.
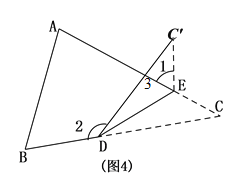
∵∠2=∠3+∠C,
∠3=∠1+∠![]() =∠1+∠C,
=∠1+∠C,
∴∠2=∠1+∠C +∠C=∠1+2∠C,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】按如图的程序进行操作,规定:程序运行从“输入一个值x”到“结果是否>487?”为一次操作. ①如果输入x的值为5,那么操作进行______次才停止.
②如果输入x的值为2k-1,并且操作进行四次才停止,那么k的最大值是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
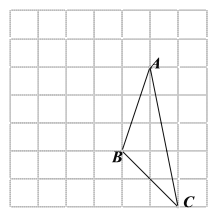
【题目】画图(只能借助于网格)并填空:
如图,每个小正方形的边长为![]() 个单位,每个小正方形的顶点叫格点.
个单位,每个小正方形的顶点叫格点.
(1)将![]() 向左平移
向左平移![]() 格,再向上平移
格,再向上平移![]() 格,请在图中画出平移后的
格,请在图中画出平移后的![]() ;
;
(2)![]() 的面积为 ;
的面积为 ;
(3)利用网格在图中画出△ABC的中线![]() ,高线
,高线![]() ;
;
(4)在图中能使![]() 的格点
的格点![]() 的个数有 个(点
的个数有 个(点![]() 异于
异于![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,一次函数的图象经过点A(2,3)与点B(0,5).
(1)求此一次函数的表达式;
(2)若点P为此一次函数图象上一点,且△POB的面积为10,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读与思考:
阅读理解问题——代数问题几何化 1.阅读理解以下文字: 我们知道,多项式的因式分解就是将一个多项式化成几个整 式的积的形式.通过因式分解,我们常常将一个次数比较高 的多项式转化成几个次数较低的整式的积,来达到降次化简 的目的.这个思想可以引领我们解决很多相对复杂的代数问 题.
例如:方程 2x2+3x=0 就可以这样来解:
解:原方程可化为 x(2x+3)=0,
所以x=0 或者 2x+3=0.
解方程 2x+3=0,得 x=-![]() . ∴原方程的解为 x=0或x=-
. ∴原方程的解为 x=0或x=-![]() .
.
根据你的理解,结合所学知识,解决以下问题:
(1)解方程:3x2-x=0
(2)解方程:(x+3)2-4x2=0;
(3)已知△ABC 的三边长为 4,x,y,请你判断代数式y2 -8y+16-x2的值的符号.
查看答案和解析>>
科目:初中数学 来源: 题型:
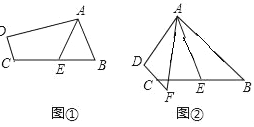
【题目】(1)如图①,在四边形ABCD中,AB∥DC,E是BC的中点,若AE是∠BAD的平分线,求证:AD=DC+AB,
(2)如图②,在四边形ABCD中,AB∥DC,F是DC延长线上一点,连接AF,E是BC的中点,若AE是∠BAF的平分线,求证:AB=AF+CF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市对初二综合素质测评中的审美与艺术进行考核,规定如下:考核综合评价得分由测试成绩(满分100分)和平时成绩(满分100分)两部分组成,其中测试成绩占80%,平时成绩占20%,并且当综合评价得分大于或等于80分时,该生综合评价为A等.
(1)孔明同学的测试成绩和平时成绩两项得分之和为185分,而综合评价得分为91分,则孔明同学测试成绩和平时成绩各得多少分?
(2)某同学测试成绩为70分,他的综合评价得分有可能达到A等吗?为什么?
(3)如果一个同学综合评价要达到A等,他的测试成绩至少要多少分?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com