
【题目】如图,在△ABC中,O是AC上一动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.若点O运动到AC的中点,则∠ACB=_____°时,四边形AECF是正方形.

 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:
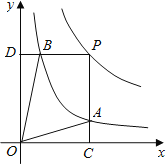
【题目】函数y=![]() 和y=
和y=![]() 在第一象限内的图象如图,点P是y=
在第一象限内的图象如图,点P是y=![]() 的图象上一动点,PC⊥x轴于点C,交y=
的图象上一动点,PC⊥x轴于点C,交y=![]() 的图象于点B.给出如下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④CA=
的图象于点B.给出如下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④CA=![]() AP.其中所有正确结论的序号是( )
AP.其中所有正确结论的序号是( )
A. ①②③ B. ②③④ C. ①③④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,,点D是边AB上一点,E为AC的中点,过点C作CF∥AB, 交DE的延长线于点F。
(1)求证:DE=FE;
(2)若CD=CF,∠A=40°,求∠BCD的度数。

查看答案和解析>>
科目:初中数学 来源: 题型:
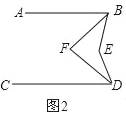
【题目】已知,直线AB∥CD
(1)如图1,点E在直线BD的左侧,猜想∠ABE、∠CDE、∠BED的数量关系,并证明你的结论;
(2)如图2,点E在直线BD的左侧,BF、DF分别平分∠ABE、∠CDE,猜想∠BFD和∠BED的数量关系,并证明你的结论;
(3)如图3,点E在直线BD的右侧,BF、DF分别平分∠ABE、∠CDE;那么第(2)题中∠BFD和∠BED的数量关系的猜想是否仍成立?如果成立,请证明;如果不成立,请写出你的猜想,并证明.


查看答案和解析>>
科目:初中数学 来源: 题型:
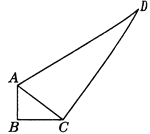
【题目】一个零件的形状如图所示,工人师傅按规定做得∠B=90°,
AB=3,BC=4,CD=12,AD=13,假如这是一块钢板,你能帮工人师傅计算一下这块钢板的面积吗?
【答案】面积等于36
【解析】试题分析:利用勾股定理求AC,再利用勾股定理逆定理求∠ACB=90°,分别求![]() 的面积.
的面积.
试题解析:
![]() ∠B=90°,AB=3,BC=4,AC=
∠B=90°,AB=3,BC=4,AC=![]()
![]() =169,
=169,
所以∠ACD=90°,
![]() .
.
所以面积是36.
【题型】解答题
【结束】
22
【题目】如图,在所给正方形网格(每个小网格的边长是1)图中完成下列各题.
(1)格点△ABC(顶点均在格点上)的面积=_________;
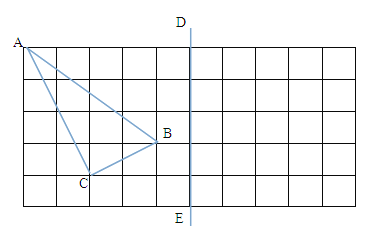
(2)画出格点△ABC关于直线DE对称的△A1B1C1;
(3)在DE上画出点P,使PB+PC最小,并求出这个最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在所给正方形网格(每个小网格的边长是1)图中完成下列各题.
(1)格点△ABC(顶点均在格点上)的面积=_________;

(2)画出格点△ABC关于直线DE对称的△A1B1C1;
(3)在DE上画出点P,使PB+PC最小,并求出这个最小值.
【答案】(1)面积等于5(2)图形见解析(3)最小值是根号17
【解析】试题分析:(1)利用勾股定理求出三角形边长,并证明是直角三角形求面积.(2)画出A,B,C的对称点A1,B2,C3,连接三角形.(3)利用对称利用两点之间直线最短求最小值.
试题解析:
(1)分别利用勾股定理求得AC=2![]() ,AB=
,AB=![]() ,BC=
,BC=![]() ,
, ![]() ,所以∠ACB=90°,面积等于
,所以∠ACB=90°,面积等于![]() =5.
=5.
(2)画出A,B,C的对称点A1,B2,C3,连接三角形.如下图.

(3)作B点对称B’,连接B’C交DE于P,B’P+PC=BP+CP,所以使PB+PC最小.
利用勾股定理B’C=![]() ,
,
所以最小值是根号17.

点睛:平面上最短路径问题
(1)归于“两点之间的连线中,线段最短”.凡属于求“变动的两线段之和的最小值”时,大都应用这一模型.
(2)归于“三角形两边之差小于第三边”.凡属于求“变动的两线段之差的最大值”时,大都应用这一模型.
(3)平面图形中,直线同侧两点到直线上一点距离之和最短问题.

【题型】解答题
【结束】
23
【题目】已知一次函数y=kx+7的图像经过点A(2,3).
(1)求k的值;
(2)判断点B(-1,8),C(3,1)是否在这个函数的图像上,并说明理由;
(3)当-3<x<-1时,求y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知2辆A型车和1辆B型车载满货物一次可运货10吨.用1辆A型车和2辆B型车载满货物一次可运货11吨.某物流公司现有31吨货物,计划同时租用A型车a辆和B型车b辆,一次运完,且每辆车都满载货物.根据以上信息解答下列问题:
(1)1辆A型车和1辆B型车载满货物一次分别可运货物多少吨?
(2)请帮助物流公司设计租车方案
(3)若A型车每辆车租金每次100元,B型车每辆车租金每次120元.请选出最省钱的租车方案,并求出最少的租车费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知平行于y轴的动直线a的表达式为x=t,直线b的表达式为y=x,直线c的表达式为y=﹣![]() x+2,且动直线a分别交直线b、c于点D、E(E在D的上方),P是y轴上一个动点,且满足△PDE是等腰直角三角形,则点P的坐标是________.
x+2,且动直线a分别交直线b、c于点D、E(E在D的上方),P是y轴上一个动点,且满足△PDE是等腰直角三角形,则点P的坐标是________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com