
【题目】如图,在所给正方形网格(每个小网格的边长是1)图中完成下列各题.
(1)格点△ABC(顶点均在格点上)的面积=_________;

(2)画出格点△ABC关于直线DE对称的△A1B1C1;
(3)在DE上画出点P,使PB+PC最小,并求出这个最小值.
【答案】(1)面积等于5(2)图形见解析(3)最小值是根号17
【解析】试题分析:(1)利用勾股定理求出三角形边长,并证明是直角三角形求面积.(2)画出A,B,C的对称点A1,B2,C3,连接三角形.(3)利用对称利用两点之间直线最短求最小值.
试题解析:
(1)分别利用勾股定理求得AC=2![]() ,AB=
,AB=![]() ,BC=
,BC=![]() ,
, ![]() ,所以∠ACB=90°,面积等于
,所以∠ACB=90°,面积等于![]() =5.
=5.
(2)画出A,B,C的对称点A1,B2,C3,连接三角形.如下图.

(3)作B点对称B’,连接B’C交DE于P,B’P+PC=BP+CP,所以使PB+PC最小.
利用勾股定理B’C=![]() ,
,
所以最小值是根号17.

点睛:平面上最短路径问题
(1)归于“两点之间的连线中,线段最短”.凡属于求“变动的两线段之和的最小值”时,大都应用这一模型.
(2)归于“三角形两边之差小于第三边”.凡属于求“变动的两线段之差的最大值”时,大都应用这一模型.
(3)平面图形中,直线同侧两点到直线上一点距离之和最短问题.

【题型】解答题
【结束】
23
【题目】已知一次函数y=kx+7的图像经过点A(2,3).
(1)求k的值;
(2)判断点B(-1,8),C(3,1)是否在这个函数的图像上,并说明理由;
(3)当-3<x<-1时,求y的取值范围.
科目:初中数学 来源: 题型:
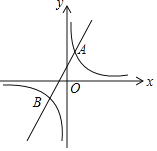
【题目】已知反比例函数y1=![]() 的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2).
的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2).
(1)求这两个函数的表达式;
(2)根据图象直接写出一次函数的值大于反比例函数的值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,O是AC上一动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.若点O运动到AC的中点,则∠ACB=_____°时,四边形AECF是正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO,如果AB=4,AO=6![]() ,那么AC=_____.
,那么AC=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】西瓜经营户以2元/千克的价格购进一批小型西瓜,以3元/千克的价格出售,每天可售出200千克.为了促销,该经营户决定降价销售.经调查发现,这种小型西瓜每降价0.1元/千克,每天可多售出40千克.另外,每天的房租等固定成本共24元,为了减少库存,该经营户要想每天盈利200元,应将每千克小型西瓜的售价降低( )元.
A.0.2或0.3
B.0.4
C.0.3
D.0.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为建设资源节约型、环境友好型社会,克服因干旱而造成的电力紧张困难,切实做好节能减排工作.某地决定对居民家庭用电实行“阶梯电价”,电力公司规定:居民家庭每月用电量在80千瓦时以下(含80千瓦时,1千瓦时俗称1度)时,实行“基本电价”;当居民家庭月用电量超过80千瓦时时,超过部分实行“提高电价”.
(1)小张家今年2月份用电100千瓦时,上缴电费68元;5月份用电120千瓦时,上缴电费88元.求“基本电价”和“提高电价”分别为多少元/千瓦时;
(2)若6月份小张家预计用电130千瓦时,请预算小张家6月份应上缴的电费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,AC=3,BC=4,点D是AB的中点,点E在DC的延长线上,且CE=![]() CD,过点B作BF∥DE交AE的延长线于点F,交AC的延长线于点G.
CD,过点B作BF∥DE交AE的延长线于点F,交AC的延长线于点G.
(1)求证:AB=BG;
(2)若点P是直线BG上的一点,试确定点P的位置,使△BCP与△BCD相似.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com