
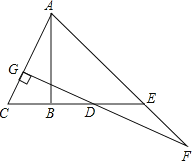
【题目】如图,AB垂直平分线段CD(AB>CD),点E是线段CD延长线上的一点,且BE=AB,连接AC,过点D作DG⊥AC于点G,交AE的延长线与点F.
(1)若∠CAB=α,则∠AFG= (用α的代数式表示);
(2)线段AC与线段DF相等吗?为什么?
(3)若CD=6,求EF的长.
【答案】(1)45°﹣α;(2)相等,理由见解析;(3)EF=3![]() .
.
【解析】
(1)根据等腰三角形的性质得到∠BAE=∠AEB=45°,根据三角形的内角和即可得到结论;
(2)连接AD,根据线段垂直平分线的性质得到AC=AD,求得∠ADC=∠ACB=α,于是得到AC=DF;
(3)根据已知条件得到BD=CB=3,过F作FH⊥CE交CE的延长线于H,得到△EHF是等腰直角三角形,求得FH=HE,根据全等三角形的性质即可得到结论.
解:(1)∵AB⊥CD,
∴∠ABE=90°,
∵AB=BE,
∴∠BAE=∠AEB=45°,
∵∠CAB=α,∠CDG=90°﹣(90°﹣α)=α=∠EDF.
∴∠AFG=∠AED﹣∠EDF=45°﹣α;
故答案为:45°﹣α;
(2)相等,
证明:连接AD,
∵AB垂直平分线段CD,
∴AC=AD,
∴∠ADC=∠ACB=90°﹣α,
∴∠DAE=∠ADC﹣45°=45°﹣α,
∴∠DAE=∠AFD,
∴AD=DF,
∴AC=DF;
(3)∵CD=6,
∴BD=CB=3,
过F作FH⊥CE交CE的延长线于H,
则△EHF是等腰直角三角形,
∴FH=HE,
∵∠H=∠ABC=90°,∠CAB=∠CDG=∠FDH,AC=AD=DF,
∴△ACB≌△DFH(AAS),
∴FH=CB=3,
∴EF=![]() FH=3
FH=3![]() .
.



 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:
【题目】某地电话拨号入网有两种收费方式,用户可以任选其一.
计时制:0.05元/分;
包月制:50元/月(限一部个人住宅电话上网).
此外,每一种上网方式都得加收通信费0.02元/分.
(1)某用户某月上网的时间为x小时,请你分别写出两种收费方式下该用户应该支付的费用.
(2)若某用户估计一个月内上网的时间为20小时,你认为采用哪种方式较为合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数的图像过点![]() ,
,![]() ,与
,与![]() 轴交于另一点
轴交于另一点![]() ,且对称轴是直线
,且对称轴是直线![]() .
.
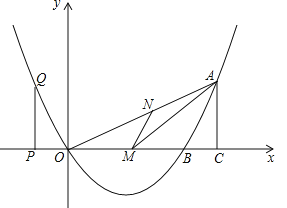
(1)求该二次函数的解析式;
(2)若![]() 是
是![]() 上的一点,作
上的一点,作![]() 交
交![]() 于
于![]() ,当
,当![]() 面积最大时,求
面积最大时,求![]() 的坐标;
的坐标;
(3)![]() 是
是![]() 轴上的点,过
轴上的点,过![]() 作
作![]() 轴,与抛物线交于
轴,与抛物线交于![]() ,过
,过![]() 作
作![]() 轴于
轴于![]() .当以
.当以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 、
、![]() 、
、![]() 为顶点的三角形相似时,求
为顶点的三角形相似时,求![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一位画家有若干个边长为![]() 的正方体,他在地面上把它们摆成如图(三层)的形式,然后,他把露出的表面都涂上颜色.
的正方体,他在地面上把它们摆成如图(三层)的形式,然后,他把露出的表面都涂上颜色.
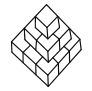
(1)图中的正方体一共有多少个?
(2)一点颜色都没涂上颜色的正方体有多少个?
(3)如果画家按此方式摆成七层,那又要多少个正方体?同样涂上颜色,又有多少个正方体没有涂上一点颜色?
查看答案和解析>>
科目:初中数学 来源: 题型:
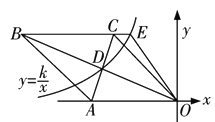
【题目】如图,菱形OABC的一边OA在x轴的负半轴上,O是坐标原点,A点坐标为(-10,0),对角线AC和OB相交于点D且AC·OB=160.若反比例函数y=![]() (x<0)的图象经过点D,并与BC的延长线交于点E,则S△OCE∶S△OAB=________.
(x<0)的图象经过点D,并与BC的延长线交于点E,则S△OCE∶S△OAB=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
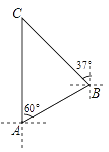
【题目】知识改变世界,科技改变生活.导航装备的不断更新极大方便了人们的出行.如图,某校组织学生乘车到黑龙滩(用C表示)开展社会实践活动,车到达A地后,发现C地恰好在A地的正北方向,且距离A地13千米,导航显示车辆应沿北偏东60°方向行驶至B地,再沿北偏西37°方向行驶一段距离才能到达C地,求B、C两地的距离.(参考数据:sin53°≈![]() ,cos53°≈
,cos53°≈![]() ,tan53°≈
,tan53°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的两边OA,OC分别在x轴和y轴上,并且OA=5,OC=3.若把矩形OABC绕着点O逆时针旋转,使点A恰好落在BC边上的A1处,则点C的对应点C1的坐标为( )
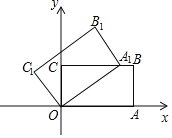
A. (﹣![]() ) B. (﹣
) B. (﹣![]() ) C. (﹣
) C. (﹣![]() ) D. (﹣
) D. (﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
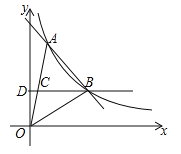
【题目】(2017山东省菏泽市,第20题,7分)如图,一次函数y=kx+b与反比例函数![]() 的图象在第一象限交于A、B两点,B点的坐标为(3,2),连接OA、OB,过B作BD⊥y轴,垂足为D,交OA于C,若OC=CA.
的图象在第一象限交于A、B两点,B点的坐标为(3,2),连接OA、OB,过B作BD⊥y轴,垂足为D,交OA于C,若OC=CA.
(1)求一次函数和反比例函数的表达式;
(2)求△AOB的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com