
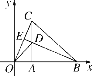
【题目】如图,在平面直角坐标系中,等腰△OBC的边OB在x轴上,OB=CB,OB边上的高CA与OC边上的高BE相交于点D,连接OD,AB=![]() ,∠CBO=45°,在直线BE上求点M,使△BMC与△ODC相似,则点M的坐标是________.
,∠CBO=45°,在直线BE上求点M,使△BMC与△ODC相似,则点M的坐标是________.
【答案】(1,![]() -1)或(-
-1)或(-![]() ,
,![]() )
)
【解析】
试题∵OB=CB,OB边上的高CA与OC边上的高BE相交于点D,AB=![]() ,∠CBO=45°,∴AB=AC=
,∠CBO=45°,∴AB=AC=![]() ,OD=CD,在Rt△BAC中,BC=
,OD=CD,在Rt△BAC中,BC=![]() =2,∴OB=2,∴OA=OB﹣AB=
=2,∴OB=2,∴OA=OB﹣AB=![]() ,在Rt△OAC中,OC=
,在Rt△OAC中,OC=![]() =
=![]() ,在Rt△OAD中,
,在Rt△OAD中,![]() ,
,![]() ,解得AD=
,解得AD=![]() ,∴OD=CD=
,∴OD=CD=![]() ,在Rt△BAD中,BD=
,在Rt△BAD中,BD=![]() =
=![]() ,①如图1,△BMC∽△CDO时,过M点作MF⊥AB于F,
,①如图1,△BMC∽△CDO时,过M点作MF⊥AB于F,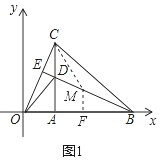
![]() ,即
,即![]() ,解得BM=
,解得BM=![]() ,∵MF⊥AB,CA是OB边上的高,∴MF∥DA,∴△BMF∽△BDA,∴
,∵MF⊥AB,CA是OB边上的高,∴MF∥DA,∴△BMF∽△BDA,∴![]() ,即
,即![]() ,解得BF=1,MF=
,解得BF=1,MF=![]() ,∴OF=OB﹣BF=1,∴点M的坐标是(1,
,∴OF=OB﹣BF=1,∴点M的坐标是(1,![]() );
);
②如图2,△BCM∽△CDO时,过M点作MF⊥AB于F,
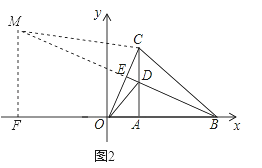
![]() ,即
,即![]() ,解得BM=
,解得BM=![]() ,∵MF⊥AB,CA是OB边上的高,∴MF∥DA,∴△BMF∽△BDA,∴
,∵MF⊥AB,CA是OB边上的高,∴MF∥DA,∴△BMF∽△BDA,∴![]() ,即
,即![]() ,解得BF=
,解得BF=![]() ,MF=
,MF=![]() ,∴OF=BF﹣OB=
,∴OF=BF﹣OB=![]() ,∴点M的坐标是(
,∴点M的坐标是(![]() ,
,![]() ).
).
综上所述,点M的坐标是(1,![]() )或(
)或(![]() ,
,![]() ).
).
故答案为:(1,![]() )或(
)或(![]() ,
,![]() ).
).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】下列各图中的MA1与NAn平行.
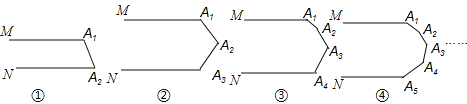
(1)图①中的∠A1+∠A2= 度,图②中的∠A1+∠A2+∠A3= 度,
图③中的∠A1+∠A2+∠A3+∠A4= 度,图④中的∠A1+∠A2+∠A3+∠A4+∠A5= 度,…,
第⑩个图中的∠A1+∠A2+∠A3+…+∠A10= 度
(2)第n个图中的∠A1+∠A2+∠A3+…+∠An= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(![]() )如图
)如图![]() ,
,![]() 中,
中,![]() ,
,![]() 是
是![]() 上任意一点,以点
上任意一点,以点![]() 为中心,取旋转角等于
为中心,取旋转角等于![]() ,把
,把![]() 逆时针旋转,画出旋转后的图形.
逆时针旋转,画出旋转后的图形.
(![]() )如图
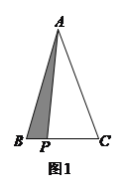
)如图![]() ,等边
,等边![]() 中,
中,![]() 为
为![]() 边上一点,
边上一点,![]() 在
在![]() 的延长线上,且
的延长线上,且![]() .
.
求证:![]() .
.
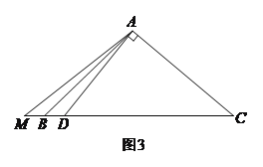
(![]() )已知:如图
)已知:如图![]() ,在
,在![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 边上一点,
边上一点,![]() 为
为![]() 延长线上一点,且
延长线上一点,且![]() ,已知
,已知![]() ,
,![]() .写出求线段
.写出求线段![]() 长的具体思路(即添加辅助线的方法,推导的具体步骤详写,其它的写出关键步骤或结果即可),并给出最后结果.
长的具体思路(即添加辅助线的方法,推导的具体步骤详写,其它的写出关键步骤或结果即可),并给出最后结果.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点B,E,C,F在一条直线上,AC∥DE,∠A=∠D,AB=DF.
(1)试说明:△ABC≌△DFE;
(2)若BF=13,EC=7,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点![]() 在反比例函数
在反比例函数![]() 的图象上,过点
的图象上,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,直线
,直线![]() 经过点
经过点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,且
,且![]() ,
,![]() .
.

(1)求反比例函数![]() 和一次函数
和一次函数![]() 的表达式;
的表达式;
(2)直接写出关于![]() 的不等式
的不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(3分)如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有( )
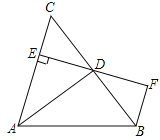
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为a的正方形的一角剪去一个边长为b的正方形,把剩余的部分(图中的阴影部分)裁剪后拼成右边的长方形.
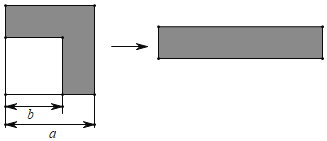
(1)请写出上述剪拼过程中所揭示的乘法公式;
(2)请运用乘法公式简便计算:20192﹣2020×2018.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在一条笔直的公路进行跑步训练,可以用如图所示一条直线上来刻画他在公路上跑步情境.假定向右跑步的路程记为正数,向左跑步的路程记为负数,则所跑步的各段路程依次记为:+5,-3,-6,+8,-6,+12,-10.(单位:百米)
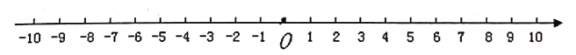
(1)小明最后是否回到出发点![]() ?
?
(2)小明在跑步过程中距离出发点![]() 最远是多少米?.
最远是多少米?.
(3)在跑步过程中,如果小明每跑1千米会消耗约60卡热量,那么小明此次训练一共会消耗多少卡?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MON=90°,OB=4,点A是直线OM上的一个动点,连结AB,作∠MAB与∠ABN的角平分线AF与BF,两条角平分线所在的直线相交于点F,则点A在运动过程中线段BF的最小值为( )
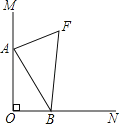
A. 4B. ![]() C. 8D. 2
C. 8D. 2![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com