【题目】将一幅三角板拼成如图所示的图形，过点C作CF平分∠DCE交DE于点F．
（1）求证：CF∥AB．
（2）求∠DFC的度数．
【答案】解：（1）证明：∵CF平分∠DCE，∴∠1=∠2=
∠DCE。
∵∠DCE=90°，∴∠1=45°。
∵∠3=45°，∴∠1=∠3。∴AB∥CF。
（2）∵∠D=30°，∠1=45°，
∴∠DFC=180°﹣30°﹣45°=105°。
【解析】
试题（1）首先根据角平分线的性质可得∠1=45°，再有∠3=45°，再根据内错角相等两直线平行可判定出AB∥CF；
（2）利用三角形内角和定理进行计算即可．
试题解析：（1）∵CF平分∠DCE，∴∠1=∠2=∠DCE，∵∠DCE=90°，∴∠1=45°，∵∠3=45°，∴∠1=∠3，∴AB∥CF（内错角相等，两直线平行）；
（2）∵∠D=30°，∠1=45°，∴∠DFC=180°﹣30°﹣45°=105°．
科目：初中数学 来源： 题型：
【题目】数学课上,张老师举了下面的例题:
例1 等腰三角形ABC中,∠A=110°,求∠B的度数.
例2 等腰三角形ABC中,∠A=40°,求∠B的度数.
张老师启发同学们进行变式,小敏编了如下一题:
变式 等腰三角形ABC中,∠A=80°,求∠B的度数.
(1)请你解答以上的变式题.
(2)解(1)后,小敏发现,∠A的度数不同,得到∠B的度数的个数也可能不同,如果在等腰三角形ABC中,设∠A=x°,当∠B有三个不同的度数时,请你探索x的取值范围.
查看答案和解析>>
科目：初中数学 来源： 题型：
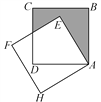
【题目】如图，将边为
的正方形ABCD绕点A沿逆时针方向旋转30°后得到正方形AEFH，则图中阴影部分的面积为( )
A. 
－
B. 3－ C. 2－ D. 2－
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，则下列结论：①ac＞0；②2a+b＞0；③y随x的增大而增大；④a﹣b+c＜0，其中正确的个数（ ）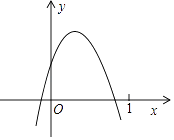
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目：初中数学 来源： 题型：
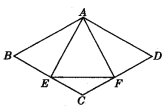
【题目】已知：如图所示，菱形ABCD中，E，F分别是CB，CD上的点，且BE=DF．
（1）试说明：AE=AF；
（2）若∠B=60°，点E，F分别为BC和CD的中点，试说明：△AEF为等边三角形．
查看答案和解析>>
科目：初中数学 来源： 题型：
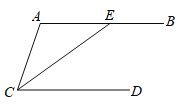
【题目】如图，∠ACE=∠AEC．
（1）若CE平分∠ACD，求证：AB∥CD．
（2）若AB∥CD，求证：CE平分∠ACD．请在（1）、（2）中选择一个进行证明．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点
在
上，点
在
上，
，
．
试说明：
，将过程补充完整．
解：∵（___________）
（___________）
∴
（___________）
∴________
__________（___________）
∴
（_____________）
又∵（___________）
∴
（___________）
∴（___________）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
