
【题目】如图所示,AB,CD交于点O,AC∥DB,AO=BO,E,F分别为OC,OD的中点,连接AF,BE,求证AF∥BE.
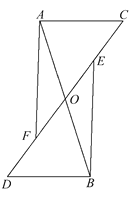
科目:初中数学 来源: 题型:
【题目】已知:在△ABC中,BC>AC,动点D绕△ABC的顶点A逆时针旋转,且AD=BC,连接DC.过AB,DC的中点E,F作直线,直线EF与直线AD,BC分别相交于点M,N.
(1)如图1,当点D旋转到BC的延长线上时,点N恰好与点F重合,取AC的中点H,连接HE,HF,根据三角形中位线定理和平行线的性质,可得∠AMF与∠ENB有何数量关系?(不需证明).
(2)当点D旋转到图2或图3中的位置时,∠AMF与∠ENB有何数量关系?请分别写出猜想,并任选一种情况证明.
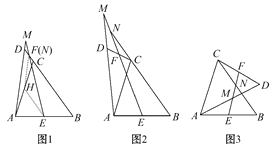
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在东西向的马路上有一个巡岗亭A,巡岗员甲从岗亭A出发以13km/h速度匀速来回巡逻,如果规定向东巡逻为正,向西巡逻为负,巡逻情况记录如下:(单位:千米)
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
4 | -5 | 3 | -4 | -3 | 6 | -1 |
(1)求第六次结束时甲的位置(在岗亭A的东边还是西边?距离多远?)
(2)在第几次结束时距岗亭A最远?距离A多远?
(3)巡逻过程中配置无线对讲机,并一直与留守在岗亭A的乙进行通话,问在甲巡逻过程中,甲与乙的保持通话时长共多少小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:① 平方等于64的数是8;② 若a,b互为相反数,ab≠0,则![]() ;③ 若
;③ 若![]() ,则
,则![]() 的值为负数;④ 若ab≠0,则
的值为负数;④ 若ab≠0,则![]() 的取值在0,1,2,-2这四个数中,不可取的值是0.正确的个数为( )
的取值在0,1,2,-2这四个数中,不可取的值是0.正确的个数为( )
A. 0个B. 1个C. 2个D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从A、B两地同时出发匀速相向而行,大楼C位于AB之间,甲与乙相遇在AC中点处,然后两车立即掉头,以原速原路返回,直到各自回到出发点.设甲、乙两车距大楼C的距离之和为y(千米),甲车离开A地的时间为t(小时),y与t的函数图象所示,则第21小时时,甲乙两车之间的距离为千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备从甲乙两位选手中选择一位选手代表学校参加所在地区的汉字听写大赛,学校对两位选手从表达能力、阅读理解、综合素质和汉字听写四个方面做了测试,他们各自的成绩(百分制)如表:
选手 | 表达能力 | 阅读理解 | 综合素质 | 汉字听写 |
甲 | 85 | 78 | 85 | 73 |
乙 | 73 | 80 | 82 | 83 |
(1)由表中成绩已算得甲的平均成绩为80.25,请计算乙的平均成绩,从他们的这一成绩看,应选派谁;
(2)如果表达能力、阅读理解、综合素质和汉字听写分别赋予它们2、1、3和4的权,请分别计算两名选手的平均成绩,从他们的这一成绩看,应选派谁.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的有( )
①不相交的两条直线是平行线;
②经过直线外一点,有且只有一条直线与这条直线平行;
③两条直线被第三条直线所截,同旁内角互补;
④在同一平面内,若直线![]() ,则直线
,则直线![]() 与
与![]() 平行.
平行.
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com