
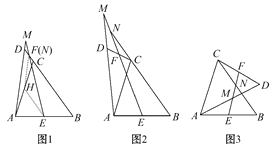
【题目】已知:在△ABC中,BC>AC,动点D绕△ABC的顶点A逆时针旋转,且AD=BC,连接DC.过AB,DC的中点E,F作直线,直线EF与直线AD,BC分别相交于点M,N.
(1)如图1,当点D旋转到BC的延长线上时,点N恰好与点F重合,取AC的中点H,连接HE,HF,根据三角形中位线定理和平行线的性质,可得∠AMF与∠ENB有何数量关系?(不需证明).
(2)当点D旋转到图2或图3中的位置时,∠AMF与∠ENB有何数量关系?请分别写出猜想,并任选一种情况证明.
【答案】(1)∠AMF=∠ENB;(2)∠AMF=∠ENB,∠AMF+∠ENB=180°,证明见解析.
【解析】
(1) 取AC的中点H,连接HE、HF,当点D旋转到图2中的位置时,由F为DC的中点,E为AB的中点,根据三角形中位线的性质得到FH∥AD,且FH=![]() AD;HE∥BC,且HE=
AD;HE∥BC,且HE=![]() BC,得到∠HFE=∠AMF,∠HEF=∠ENB,HE=HF,则∠HEF=∠HFE,所以∠AMF=∠BNE;当点D旋转到图3中的位置时,同理可证得∠AMF=∠BNE.
BC,得到∠HFE=∠AMF,∠HEF=∠ENB,HE=HF,则∠HEF=∠HFE,所以∠AMF=∠BNE;当点D旋转到图3中的位置时,同理可证得∠AMF=∠BNE.
(2) 与(1)相同,都需要作出两条辅助线,两次运用中位线定理解答.
(1)图1:∠AMF=∠ENB.
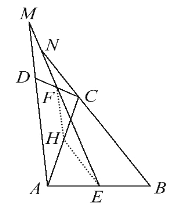
(2)图2:∠AMF=∠ENB;
图3:∠AMF+∠ENB=180°.
当点D旋转到图2中的位置时,
证明:如图,取AC的中点H,
连接HE,HF.
∵F是DC的中点,H是AC的中点,
∴HF∥AD,HF=![]() AD,
AD,
∴∠AMF=∠HFE,
同理,HE∥CB,HE=![]() CB,∴∠ENB=∠HEF.
CB,∴∠ENB=∠HEF.
∵AD=BC,∴HF=HE,∴∠HEF=∠HFE,
∴∠ENB=∠AMF.
当点D旋转到图3中的位置时,
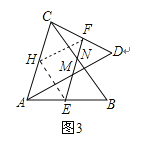
用同样的方法可证明∠HFE=∠AME,∠HEF=∠BNE,
而∠HFE=∠HEF,
∴∠AME=∠BNE,
而∠AMF+∠AME=180°,
∴∠AMF+∠BNE=180°.
故答案为:∠AMF=∠BNE或∠AMF+∠BNE=180°.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
【题目】如图所示,点C是线段AB上的一点,点D是线段AB的中点,点E是线段BC的中点.
(1)当AC=8,BC=6时,求线段DE的长度;
(2)当AC=m,BC=n(m>n)时,求线段DE的长度;
(3)从(1)(2)的结果中,你发现了什么规律?请直接写出来.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,张老师举了下面的例题:
例1 等腰三角形ABC中,∠A=110°,求∠B的度数.
例2 等腰三角形ABC中,∠A=40°,求∠B的度数.
张老师启发同学们进行变式,小敏编了如下一题:
变式 等腰三角形ABC中,∠A=80°,求∠B的度数.
(1)请你解答以上的变式题.
(2)解(1)后,小敏发现,∠A的度数不同,得到∠B的度数的个数也可能不同,如果在等腰三角形ABC中,设∠A=x°,当∠B有三个不同的度数时,请你探索x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某市举办的“读好书,讲礼仪”活动中,东华学校积极行动,各班图书角的新书、好书不断增多,除学校购买外,还有师生捐献的图书.下面是七年级(1)班全体同学捐献图书的情况统计图:
请你根据以上统计图中的信息,解答下列问题:
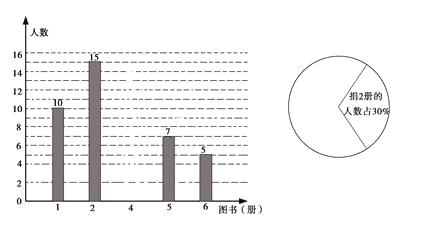
(1)该班有学生多少人?
(2)补全条形统计图;
(3)七(1)班全体同学所捐献图书的中位数和众数分别是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线a∥b,且a与b之间的距离为4,点A到直线a的距离为2,点B到直线b的距离为3,AB![]() .试在直线a上找一点M,在直线b上找一点N,满足MN⊥a且AM+MN+NB的长度和最短,则此时AM+NB=( )
.试在直线a上找一点M,在直线b上找一点N,满足MN⊥a且AM+MN+NB的长度和最短,则此时AM+NB=( )
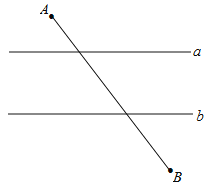
A. 6 B. 8 C. 10 D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD,AN.

(1)求证:四边形AMDN是平行四边形;
(2)填空:①当AM的值为 时,四边形AMDN是矩形;②当AM的值为 时,四边形AMDN是菱形。
查看答案和解析>>
科目:初中数学 来源: 题型:
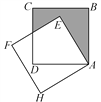
【题目】如图,将边为![]() 的正方形ABCD绕点A沿逆时针方向旋转30°后得到正方形AEFH,则图中阴影部分的面积为( )
的正方形ABCD绕点A沿逆时针方向旋转30°后得到正方形AEFH,则图中阴影部分的面积为( )
A. ![]() -
-![]() B. 3-
B. 3-![]() C. 2-
C. 2-![]() D. 2-
D. 2-![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com