
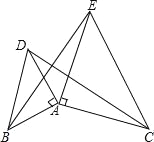
【题目】如图,已知AB=AD,AC=AE,∠BAD=∠CAE=90°,试判断CD与BE的大小关系和位置关系,并进行证明.
科目:初中数学 来源: 题型:
【题目】甲乙两人在相同条件下各射靶10次,甲10次射靶的成绩的情况如图所示,乙10次射靶的成绩依次是:3环、4环、5环、8环、7环、7环、8环、9环、9环、10环.
(1)请在图中画出乙的射靶成绩的折线图;
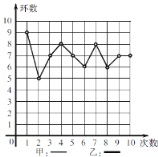
(2) 请从下列两个不同角度对这次测试结果进行分析.
①从平均数和方差相结合看(分析谁的成绩稳定些);
②从平均数和中位数相结合看(分析谁的成绩好些).
查看答案和解析>>
科目:初中数学 来源: 题型:
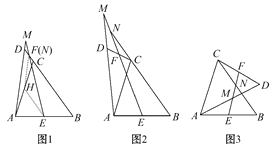
【题目】已知:在△ABC中,BC>AC,动点D绕△ABC的顶点A逆时针旋转,且AD=BC,连接DC.过AB,DC的中点E,F作直线,直线EF与直线AD,BC分别相交于点M,N.
(1)如图1,当点D旋转到BC的延长线上时,点N恰好与点F重合,取AC的中点H,连接HE,HF,根据三角形中位线定理和平行线的性质,可得∠AMF与∠ENB有何数量关系?(不需证明).
(2)当点D旋转到图2或图3中的位置时,∠AMF与∠ENB有何数量关系?请分别写出猜想,并任选一种情况证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的面积为16,BC=8.现将△ABC沿直线BC向右平移a个单位到△DEF的位置.
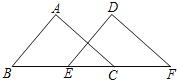
(1)当△ABC所扫过的面积为32时,求a的值;
(2)连接AE、AD,当AB=5,a=5时,试判断△ADE的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,△ABC,∠ACB=90°,∠B=2∠A.
(1)用直尺和圆规作△ABC的角平分线BD,保留作图痕迹;
(2)在(1)的基础上,求∠ADB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线y= ![]() x2﹣
x2﹣ ![]() x+3
x+3 ![]() 与x轴交于点A、B两点(点A在点B的左侧),与y轴交于点C,过点C作CD∥x轴,且交抛物线于点D,连接AD,交y轴于点E,连接AC.
与x轴交于点A、B两点(点A在点B的左侧),与y轴交于点C,过点C作CD∥x轴,且交抛物线于点D,连接AD,交y轴于点E,连接AC.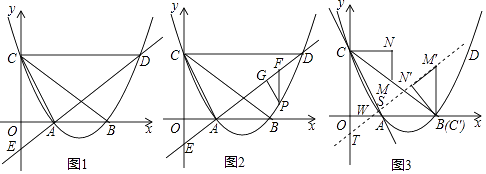
(1)求S△ABD的值;
(2)如图2,若点P是直线AD下方抛物线上一动点,过点P作PF∥y轴交直线AD于点F,作PG∥AC交直线AD于点G,当△PGF的周长最大时,在线段DE上取一点Q,当PQ+ ![]() QE的值最小时,求此时PQ+
QE的值最小时,求此时PQ+ ![]() QE的值;
QE的值;
(3)如图3,M是BC的中点,以CM为斜边作直角△CMN,使CN∥x轴,MN∥y轴,将△CMN沿射线CB平移,记平移后的三角形为△C′M′N′,当点N′落在x轴上即停止运动,将此时的△C′M′N′绕点C′逆时针旋转(旋转度数不超过180°),旋转过程中直线M′N′与直线CA交于点S,与y轴交于点T,与x轴交于点W,请问△CST是否能为等腰三角形?若能,请求出所有符合条件的WN′的长度;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com