
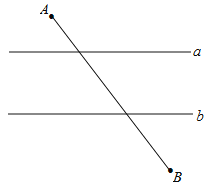
【题目】如图,已知直线a∥b,且a与b之间的距离为4,点A到直线a的距离为2,点B到直线b的距离为3,AB![]() .试在直线a上找一点M,在直线b上找一点N,满足MN⊥a且AM+MN+NB的长度和最短,则此时AM+NB=( )
.试在直线a上找一点M,在直线b上找一点N,满足MN⊥a且AM+MN+NB的长度和最短,则此时AM+NB=( )
A. 6 B. 8 C. 10 D. 12
【答案】B
【解析】
MN表示直线a与直线b之间的距离,是定值,只要满足AM+NB的值最小即可.过A作直线a的垂线,并在此垂线上取点A′,使得AA′=MN,连接A'B,则A'B与直线b的交点即为N,过N作MN⊥a于点M.则A'B为所求,利用勾股定理可求得其值.
过A作直线a的垂线,并在此垂线上取点A′,使得AA′=4,连接A′B,与直线b交于点N,过N作直线a的垂线,交直线a于点M,连接AM,过点B作BE⊥AA′,交射线AA′于点E,如图,∵AA′⊥a,MN⊥a,∴AA′∥MN.
又∵AA′=MN=4,∴四边形AA′NM是平行四边形,∴AM=A′N.
由于AM+MN+NB要最小,且MN固定为4,所以AM+NB最小.
由两点之间线段最短,可知AM+NB的最小值为A′B.
∵AE=2+3+4=9,AB![]() ,∴BE
,∴BE![]() .
.
∵A′E=AE﹣AA′=9﹣4=5,∴A′B![]() 8.
8.
所以AM+NB的最小值为8.
故选B.


科目:初中数学 来源: 题型:
【题目】如图,在10×10的网格中,每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.若抛物线经过图中的三个格点,则以这三个格点为顶点的三角形称为抛物线的“内接格点三角形”.以O为坐标原点建立如图所示的平面直角坐标系,若抛物线与网格对角线OB的两个交点之间的距离为 ![]() ,且这两个交点与抛物线的顶点是抛物线的内接格点三角形的三个顶点,则满足上述条件且对称轴平行于y轴的抛物线条数是( )
,且这两个交点与抛物线的顶点是抛物线的内接格点三角形的三个顶点,则满足上述条件且对称轴平行于y轴的抛物线条数是( )
A.16
B.15
C.14
D.13
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某公司有三个住宅区可看作一点,A,B,C各区分别住有职工30人、15人、10人,且这三个住宅区在一条大道上(A,B,C三点共线),已知AB=100米,BC=200米.为了方便职工上下班,该公司的接送车打算在此间只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在( )
![]()
A. 点A B. 点B
C. A,B之间 D. B,C之间
查看答案和解析>>
科目:初中数学 来源: 题型:
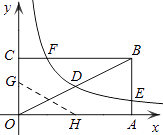
【题目】如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(4,n)在边AB上,反比例函数 ![]() (k≠0)在第一象限内的图象经过点D、E,且tan∠BOA=
(k≠0)在第一象限内的图象经过点D、E,且tan∠BOA= ![]() .
.
(1)求边AB的长;
(2)求反比例函数的解析式和n的值;
(3)若反比例函数的图象与矩形的边BC交于点F,将矩形折叠,使点O与点F重合,折痕分别与x、y轴正半轴交于点H、G,求线段OG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平安加气站某日8:00的储气量为10 000立方米.从8:00开始,3把加气枪同时以每车20立方米的加气量,依次给在加气站排队等候的若干辆车加气.8:30时,为缓解排队压力,又增开了2把加气枪.假设加气过程中每把加气枪加气的速度是匀速的,在不关闭加气枪的情况下,加气站的储气量![]() (立方米)与时间
(立方米)与时间![]() (小时)之间的函数关系如图中的折线
(小时)之间的函数关系如图中的折线![]() 所示.
所示.
(1)分别求出8:00 ~8:30及8:30之后加气站的储气量![]() (立方米)与时间
(立方米)与时间![]() (小时)之间的函数表达式.
(小时)之间的函数表达式.
(2)前30辆车能否在当天8:42之前加完气?
(3)若前![]() 辆车按上述方式加气,它们加完气的时间要比不增开加气枪加完气的时间提前1个小时,求
辆车按上述方式加气,它们加完气的时间要比不增开加气枪加完气的时间提前1个小时,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将斜边长为4的直角三角板放在直角坐标系xOy中,两条直角边分别与坐标轴重合,P为斜边的中点.现将此三角板绕点O顺时针旋转120°后点P的对应点的坐标是( )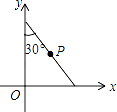
A.( ![]() ,1)
,1)
B.(1,﹣ ![]() )
)
C.(2 ![]() ,﹣2)
,﹣2)
D.(2,﹣2 ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠CAB=30°,AB=10,点D在线段AB上,AD=2.点P,Q以相同的速度从D点同时出发,点P沿DB方向运动,点Q沿DA方向到点A后立刻以原速返回向点B运动.以PQ为直径构造⊙O,过点P作⊙O的切线交折线AC﹣CB于点E,将线段EP绕点E顺时针旋转60°得到EF,过F作FG⊥EP于G,当P运动到点B时,Q也停止运动,设DP=m. 
(1)当2<m≤8时,AP=,AQ=.(用m的代数式表示)
(2)当线段FG长度达到最大时,求m的值;
(3)在点P,Q整个运动过程中, ①当m为何值时,⊙O与△ABC的一边相切?
②直接写出点F所经过的路径长是.(结果保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com