
【题目】如图,△ABC内接于⊙O,AD是∠BAC的平分线,交BC于点M,交⊙O于点D.则图中相似三角形共有( ) 
A.2对
B.4对
C.6对
D.8对
【答案】C
【解析】解:∵AD是∠BAC的平分线, ∴∠BAD=∠CAD,BD=CD,
∴∠BAD=∠CAD=∠DBC=∠DCB,
又∵∠BDA=∠MDB,∠CDA=∠MDC
∴△ABD∽△BDM;△ADC∽△CDM;
∵∠CAD=∠CBD,∠AMC=∠BMD,
∴△AMC∽△BMD,
∵∠BAD=∠MCD,∠AMB=∠CMD,
∴△ABM∽△CDM,
∵∠ABC=∠ADC,∠BAD=∠DAC,
∴△ABM∽△ADC,
∵∠ACB=∠ADB,∠BAD=∠CAD,
∴△ACM∽△ADB,
∴共有六对相似三角形,
故选:C.
【考点精析】解答此题的关键在于理解圆周角定理的相关知识,掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半,以及对相似三角形的判定的理解,了解相似三角形的判定方法:两角对应相等,两三角形相似(ASA);直角三角形被斜边上的高分成的两个直角三角形和原三角形相似; 两边对应成比例且夹角相等,两三角形相似(SAS);三边对应成比例,两三角形相似(SSS).


科目:初中数学 来源: 题型:
【题目】已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P的运动时间为t秒,当t的值为( )秒时,△ABP和△DCE全等.

A. 1 B. 1或3 C. 1或7 D. 3或7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A(0,2)、B( ![]() ,2)、C(0,4),过点C向右作平行于x轴的射线,点P是射线上的动点,连接AP,以AP为边在其左侧作等边△APQ,连接PB、BA.若四边形ABPQ为梯形,则:
,2)、C(0,4),过点C向右作平行于x轴的射线,点P是射线上的动点,连接AP,以AP为边在其左侧作等边△APQ,连接PB、BA.若四边形ABPQ为梯形,则: 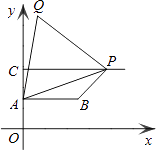
(1)当AB为梯形的底时,点P的横坐标是;
(2)当AB为梯形的腰时,点P的横坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线a∥b,且a与b之间的距离为4,点A到直线a的距离为2,点B到直线b的距离为3,AB![]() .试在直线a上找一点M,在直线b上找一点N,满足MN⊥a且AM+MN+NB的长度和最短,则此时AM+NB=( )
.试在直线a上找一点M,在直线b上找一点N,满足MN⊥a且AM+MN+NB的长度和最短,则此时AM+NB=( )
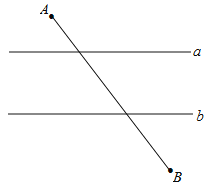
A. 6 B. 8 C. 10 D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
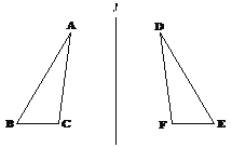
【题目】如图所示,是用笔尖扎重叠的纸得到的成轴对称的图案,请根据图形写出:
(1)两组对应点:__________和__________;
(2)两组对应线段:__________和__________;
(3)两组对应角:__________和__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=120°,AD,BE分别为△ABC的角平分线,连结DE.
(1)求证:点E到DA,DC的距离相等;
(2)求∠DEB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下述命题中,真命题有( )
(1)对角线互相垂直的四边形是菱形
(2)三个角的度数之比为1:3:4的三角形是直角三角形
(3)对角互补的平行四边形是矩形
(4)三边之比为1: ![]() :2的三角形是直角三角形.
:2的三角形是直角三角形.
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABO中,∠OAB=Rt∠,点A在x轴的正半轴,点B在第一象限,C,D分别是BO,BA的中点,点E在CD的延长线上.若函数y1= ![]() (x>0)的图象经过B,E,函数y2=
(x>0)的图象经过B,E,函数y2= ![]() (x>0)的图象过点C,且△BCE的面积为1,则k2的值为( )
(x>0)的图象过点C,且△BCE的面积为1,则k2的值为( ) 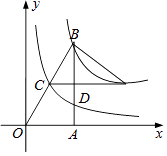
A.![]()
B.![]()
C.3
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2+bx+c与x轴交于点A(1,0)和点B,与y轴交于点C(0,﹣3).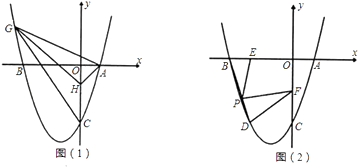
(1)求抛物线的解析式;
(2)如图(1),己知点H(0,﹣1).问在抛物线上是否存在点G (点G在y轴的左侧),使得S△GHC=S△GHA?若存在,求出点G的坐标;若不存在,请说明理由;
(3)如图(2),抛物线上点D在x轴上的正投影为点E(﹣2,0),F是OC的中点,连接DF,P为线段BD上的一点,若∠EPF=∠BDF,求线段PE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com