
【题目】如图,已知抛物线y=x2+bx+c与x轴交于点A(1,0)和点B,与y轴交于点C(0,﹣3).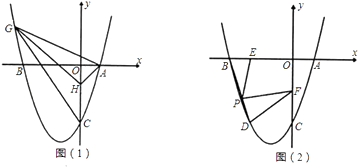
(1)求抛物线的解析式;
(2)如图(1),己知点H(0,﹣1).问在抛物线上是否存在点G (点G在y轴的左侧),使得S△GHC=S△GHA?若存在,求出点G的坐标;若不存在,请说明理由;
(3)如图(2),抛物线上点D在x轴上的正投影为点E(﹣2,0),F是OC的中点,连接DF,P为线段BD上的一点,若∠EPF=∠BDF,求线段PE的长.
【答案】
(1)
解:由题意得: ![]() ,
,
解得: ![]() ,
,
∴抛物线的解析式为:y=x2+2x﹣3
(2)
解:解法一:
假设在抛物线上存在点G,设G(m,n),显然,当n=﹣3时,△HGC不存在.
①当n>﹣3时,
可得S△GHA=﹣ ![]() +v
+v ![]() ,S△GHC=﹣m,
,S△GHC=﹣m,
∵S△GHC=S△GHA,
∴m+n+1=0,
由 ![]() ,
,
解得:  或
或 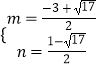 ,
,
∵点G在y轴的左侧,
∴G(﹣ ![]() ,
, ![]() );
);
②当﹣4≤n<﹣3时,
可得S△GHA= ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() ,S△GHC=﹣m,
,S△GHC=﹣m,
∵S△GHC=S△GHA,
∴3m﹣n﹣1=0,
由 ![]() ,
,
解得: ![]() 或
或 ![]() ,
,
∵点G在y轴的左侧,
∴G(﹣1,﹣4).
∴存在点G(﹣ ![]() ,
, ![]() )或G(﹣1,﹣4).
)或G(﹣1,﹣4).
解法二:
①如图①,当GH∥AC时,点A,点C到GH的距离相等,

∴S△GHC=S△GHA,
可得AC的解析式为y=3x﹣3,
∵GH∥AC,得GH的解析式为y=3x﹣1,
∴G(﹣1,﹣4);
②如图②,当GH与AC不平行时,

∵点A,C到直线GH的距离相等,
∴直线GH过线段AC的中点M( ![]() ,﹣
,﹣ ![]() ).
).
∴直线GH的解析式为y=﹣x﹣1,
∴G(﹣ ![]() ,
, ![]() ,
,
∴存在点G(﹣ ![]() ,
, ![]() )或G(﹣1,﹣4)
)或G(﹣1,﹣4)
(3)
解:解法一:
如图③,

∵E(﹣2,0),
∴D的横坐标为﹣2,
∵点D在抛物线上,
∴D(﹣2,﹣3),
∵F是OC中点,
∴F(0,﹣ ![]() ),
),
∴直线DF的解析式为:y= ![]() x﹣
x﹣ ![]() ,
,
则它与x轴交于点Q(2,0),
则QB=QD,得∠QBD=∠QDB,∠BPE+∠EPF+∠FPD=∠DFP+∠PDF+∠FPD=180°,
∵∠EPF=∠PDF,
∴∠BPE=∠DFP,
∴△PBE∽△FDP,
∴ ![]() ,
,
得:PBDP= ![]() ,
,
∵PB+DP=BD= ![]() ,
,
∴PB= ![]() ,
,
即P是BD的中点,
连接DE,
∴在Rt△DBE中,PE= ![]() BD=
BD= ![]() .
.
解法二:
可知四边形ABDC为等腰梯形,取BD的中点P′,
P′F= ![]() (OB+CD)=
(OB+CD)= ![]() ,
,
P′F∥CD∥AB,
连接EF,可知EF=DF= ![]() ,
,
即EF=FP′=FD,
即△FEP′相似△FP′D,
即∠EP′F=∠FP′D=∠FDP′,
即∠EP′F和∠EPF重合,
即P和P′重合,
P为BC中点,
PE= ![]() BD=
BD= ![]() (△BDE为直角三角形).
(△BDE为直角三角形).
【解析】(1)由抛物线y=x2+bx+c与x轴交于点A(1,0)和点B,与y轴交于点C(0,﹣3),利用待定系数法即可求得二次函数的解析式;(2)分别从GH∥AC与GH与AC不平行去分析,注意先求得直线GH的解析式,根据交点问题即可求得答案,小心不要漏解;(3)利用待定系数法求得直线DF的解析式,即可证得△PBE∽△FDP,由相似三角形的对应边成比例,即可求得答案.


科目:初中数学 来源: 题型:
【题目】2012年6月5日是“世界环境日”,南宁市某校举行了“绿色家园”演讲比赛,赛后整理参赛同学的成绩,制作成直方图(如图). 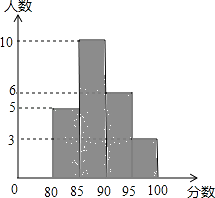
(1)分数段在范围的人数最多;
(2)全校共有多少人参加比赛?
(3)学校决定选派本次比赛成绩最好的3人参加南宁市中学生环保演讲决赛,并为参赛选手准备了红、蓝、白颜色的上衣各1件和2条白色、1条蓝色的裤子.请用“列表法”或“树形图法”表示上衣和裤子搭配的所有可能出现的结果,并求出上衣和能搭配成同一种颜色的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠CAB=30°,AB=10,点D在线段AB上,AD=2.点P,Q以相同的速度从D点同时出发,点P沿DB方向运动,点Q沿DA方向到点A后立刻以原速返回向点B运动.以PQ为直径构造⊙O,过点P作⊙O的切线交折线AC﹣CB于点E,将线段EP绕点E顺时针旋转60°得到EF,过F作FG⊥EP于G,当P运动到点B时,Q也停止运动,设DP=m. 
(1)当2<m≤8时,AP=,AQ=.(用m的代数式表示)
(2)当线段FG长度达到最大时,求m的值;
(3)在点P,Q整个运动过程中, ①当m为何值时,⊙O与△ABC的一边相切?
②直接写出点F所经过的路径长是.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲,乙两辆汽车先后从A地出发到B地,甲车出发1小时后,乙车才出发,如图所示的l1和l2表示甲,乙两车相对于出发地的距离y(km)与追赶时间x(h)之间的关系:
(1)哪条线表示乙车离出发地的距离y与追赶时间x之间的关系?
(2)甲,乙两车的速度分别是多少?
(3)试分别确定甲,乙两车相对于出发地的距离y(km)与追赶时间x(h)之间的关系式;
(4)乙车能在1.5小时内追上甲车吗?若能,说明理由;若不能,求乙车出发几小时才能追上甲?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将OA2B2变换成△OA3B3;已知变换过程中各点坐标分别为A(1,3),A1(2,3),A2(4,3),A3(8,3),B(2,0),B1(4,0),B2(8,0),B3(16,0).
(1)观察每次变换前后的三角形有何变化,找出规律,按此规律再将△OA3B3变换成△OA4B4,则A4的坐标为 ,B4的坐标为 .
(2)按以上规律将△OAB进行n次变换得到△OAnBn,则An的坐标为 ,Bn的坐标为 ;
(3)△OAnBn的面积为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有红、白两种颜色的小球(除颜色外其余都相同),其中红球3个,白球1个.
(1)求任意摸出一球是白球的概率;
(2)甲同学先随机摸出一个小球(不放回),再随机摸出一个小球,请用画树状图或列表的方法求两次摸出都是红球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形纸片ABCD置于直角坐标系中,点A(4,0),点B(0,3),点D(异于点B、C)为边BC上动点,过点O、D折叠纸片,得点B′和折痕OD.过点D再次折叠纸片,使点C落在直线DB′上,得点C′和折痕DE,连接OE,设BD=t.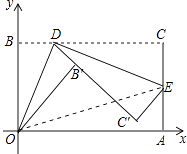
(1)当t=1时,求点E的坐标;
(2)设S四边形OECB=s,用含t的式子表示s(要求写出t的取值范围);
(3)当OE取最小值时,求点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB和CD交于点O,OE⊥AB,垂足为点O,OP平分∠EOD,∠AOD=144°.
(1)求∠AOC与∠COE的度数;
(2)求∠BOP的度数.

【答案】(1)∠AOC=36°,∠COE=54°,(2)∠BOP=27°.
【解析】
(1)由邻补角定义,可求得得∠AOC度数,由垂直定义,可得∠AOE=∠BOE=90°,由余角定义可求得∠COE;
(2)由邻补角定义可得∠DOE度数,由OO平分∠DOE,可得∠EOP度数,再由余角定义可求得∠BOP度数.
(1)∵∠AOC+∠AOD=180°,∠AOD=144°,
∴∠AOC=180°-∠AOD=180°-144°=36°,
∵OE⊥AB,
∴∠AOE=∠BOE=90°,
∴∠COE=∠AOE-∠AOC=90°-36°=54°,
(2)∵∠COE+∠DOE=180°,
∴∠DOE=180°-∠COE=180°-54°=126°,
∵OO平分∠DOE,
∴∠EOP=![]() ∠DOE=
∠DOE=![]() ×126°=63°,
×126°=63°,
∴∠BOP=∠BOE-∠EOP=90°-63°=27°.
【点睛】
本题考查了对顶角、邻补角以及垂线的性质,是基础知识要熟练掌握.
【题型】解答题
【结束】
27
【题目】如表为某市居民每月用水收费标准,(单位:元/m3).
用水量 | 单价 |
0<x≤20 | a |
剩余部分 | a+1.1 |
(1)某用户1月用水10立方米,共交水费26元,则a= 元/m3;
(2)在(1)的条件下,若该用户2月用水25立方米,则需交水费 元;
(3)在(1)的条件下,若该用户水表3月份出了故障,只有70%的用水量记入水表中,该用户3月份交了水费81.6元.请问该用户实际用水多少立方米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com