
【题目】如图,直线AB和CD交于点O,OE⊥AB,垂足为点O,OP平分∠EOD,∠AOD=144°.
(1)求∠AOC与∠COE的度数;
(2)求∠BOP的度数.

【答案】(1)∠AOC=36°,∠COE=54°,(2)∠BOP=27°.
【解析】
(1)由邻补角定义,可求得得∠AOC度数,由垂直定义,可得∠AOE=∠BOE=90°,由余角定义可求得∠COE;
(2)由邻补角定义可得∠DOE度数,由OO平分∠DOE,可得∠EOP度数,再由余角定义可求得∠BOP度数.
(1)∵∠AOC+∠AOD=180°,∠AOD=144°,
∴∠AOC=180°-∠AOD=180°-144°=36°,
∵OE⊥AB,
∴∠AOE=∠BOE=90°,
∴∠COE=∠AOE-∠AOC=90°-36°=54°,
(2)∵∠COE+∠DOE=180°,
∴∠DOE=180°-∠COE=180°-54°=126°,
∵OO平分∠DOE,
∴∠EOP=![]() ∠DOE=
∠DOE=![]() ×126°=63°,
×126°=63°,
∴∠BOP=∠BOE-∠EOP=90°-63°=27°.
【点睛】
本题考查了对顶角、邻补角以及垂线的性质,是基础知识要熟练掌握.
【题型】解答题
【结束】
27
【题目】如表为某市居民每月用水收费标准,(单位:元/m3).
用水量 | 单价 |
0<x≤20 | a |
剩余部分 | a+1.1 |
(1)某用户1月用水10立方米,共交水费26元,则a= 元/m3;
(2)在(1)的条件下,若该用户2月用水25立方米,则需交水费 元;
(3)在(1)的条件下,若该用户水表3月份出了故障,只有70%的用水量记入水表中,该用户3月份交了水费81.6元.请问该用户实际用水多少立方米?
【答案】(1)a=2.6;(2)需交水费70.5元;(3)该用户实际用水40立方米.
【解析】
(1)由单价=总价÷数量就可以得出结论;
(2)设该用户2月份水费=0<x≤20的水费+x大于20部分的水费,列出算式计算即可求解;
(3)设该用户实际用水m吨,由70%的水量的水费为81.6元=单价×数量建立方程求出其解即可.
(1)a=26÷10=2.6(元/m3);
(2)2.6×20+(2.6+1.1)×(25-20)
=52+3.7×5
=52+18.5
=70.5(元).
答:需交水费70.5元;
(3)设该用户实际用水m立方米,
由题意,得2.6×20+(2.6+1.1)×(70%m-20)=81.6,
解得:m=40.
故该用户实际用水40立方米.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2+bx+c与x轴交于点A(1,0)和点B,与y轴交于点C(0,﹣3).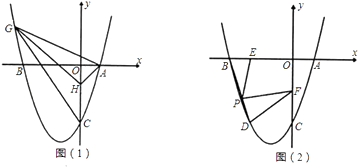
(1)求抛物线的解析式;
(2)如图(1),己知点H(0,﹣1).问在抛物线上是否存在点G (点G在y轴的左侧),使得S△GHC=S△GHA?若存在,求出点G的坐标;若不存在,请说明理由;
(3)如图(2),抛物线上点D在x轴上的正投影为点E(﹣2,0),F是OC的中点,连接DF,P为线段BD上的一点,若∠EPF=∠BDF,求线段PE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+4A(1,﹣1),B(5,﹣1),与y轴交于点C. 
(1)求抛物线的函数表达式;
(2)如图1,连接CB,若点P在直线BC上方的抛物线上,△BCP的面积为15,求点P的坐标;
(3)如图2,⊙O1过点A、B、C三点,AE为直径,点M为弧ACE上的一动点(不与点A,E重合),∠MBN为直角,边BN与ME的延长线交于N,求线段BN长度的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据要求完成下列题目:
(1)图中有_____块小正方体;
(2)请在下面方格纸中分别画出它的主视图、左视图和俯视图;
(3)用小正方体搭一几何体,使得它的俯视图和左视图与你在图方格中所画的图一致,若这样的几何体最少要m个小正方体,最多要n个小正方体,则m+n的值为____.

【答案】(1)7;(2)画图见解析;(3)16
【解析】
(1)直接根据立体图形得出小正方体的个数;
(2)主视图从左往右小正方形的个数为1,3,2;左视图从左往右小正方形的个数为3,1;俯视图从左往右小正方形的个数1,2,1;
(3)由俯视图易得最底层小立方块的个数,由左视图找到其余层数里最少个数和最多个数相加即可.
(1)图中有7块小正方体;
故答案为:7;
(2)如图所示:
 ;
;
(3)用小立方体搭一几何体,使得它的俯视图和左视图与你在上图方格中所画的图一致,则这样的几何体最少要6个小立方块,最多要10个小立方块.则m+n=16
故答案为:16
【点睛】
此题主要考查了三视图,用到的知识点为:三视图分为主视图、左视图、俯视图,分别是从物体正面、左面和上面看,所得到的图形;俯视图决定底层立方块的个数,易错点是由主视图得到其余层数里最少的立方块个数和最多的立方块个数.
【题型】解答题
【结束】
24
【题目】如图,点P是∠AOB的边OA上的一点,作∠AOB的平分线ON;
(1)过点P画OB的平行线交ON于点M;
(2)过点M画OB的垂线,垂足为H;
(3)度量线段PO、PM与MH的长度,会发现:线段PO与PM的大小关系是 ;线段MH与PM的大小关系是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=13,BC=14.
(1)如图1,AD⊥BC于点D,且BD=5,则△ABC的面积为 ;
(2)在(1)的条件下,如图2,点H是线段AC上任意一点,分别过点A,C作直线BH的垂线,垂足为E,F,设BH=x,AE=m,CF=n,请用含x的代数式表示m+n,并求m+n的最大值和最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有四张外观质地相同的扑克牌,其中两张A,两张K 
(1)把四张牌放成两堆,每堆一张A一张K,把它们正面朝下放置,随机在这两堆中各抽一张牌,请通过画树状图或列表计算,抽出的两张牌正好是一张A一张K的概率?
(2)元芳说:把这四张牌混在一起,正面朝下放置,从中任意抽取两张牌,结果是一张A一张K的概率与(1)中的概率相等,元芳说得对吗?请计算说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,A、B在数轴上对应的数分别用a、b表示,且(a﹣20)2+|b+10|=0,P是数轴上的一个动点.
(1)在数轴上标出A、B的位置,并求出A、B之间的距离;
(2)已知线段OB上有点C且|BC|=6,当数轴上有点P满足PB=2PC时,求P点对应的数;
(3)动点P从原点开始第一次向左移动1个单位长度,第二次向右移动3个单位长度,第三次向左移动5个单位长度,第四次向右移动7个单位长度,…….点P能移动到与A或B重合的位置吗?若不能,请直接回答;若能,请直接指出,第几次移动,与哪一点重合.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A路口的交通信号灯依次显示为红灯亮20秒,绿灯亮40秒,再红灯亮20秒,绿灯亮40秒,如此连续不断循环显示下去…
(1)求A路口显示红灯的概率.
(2)小亮上班路上会遇到A,B两个路口,B路口红绿灯的显示方式和A路口完全相同,求他在上班路上两次都遇到红灯的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com