
【题目】A路口的交通信号灯依次显示为红灯亮20秒,绿灯亮40秒,再红灯亮20秒,绿灯亮40秒,如此连续不断循环显示下去…
(1)求A路口显示红灯的概率.
(2)小亮上班路上会遇到A,B两个路口,B路口红绿灯的显示方式和A路口完全相同,求他在上班路上两次都遇到红灯的概率.
【答案】
(1)解:∵交通信号灯红灯亮20秒,绿灯亮40秒,
∴A路口显示红灯的概率为 ![]() =
= ![]() ;
;
(2)解:将绿灯亮起的时间划分为第1个20秒和第2个20秒,记作绿1、绿2,
画树状图如下:
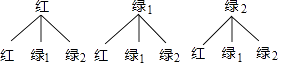
则共有9种等可能结果,每种结果出现的可能性相等,
其中两次都是红灯的有1种,
∴他在上班路上两次都遇到红灯的概率为 ![]() .
.
【解析】(1)根据概率公式,用红灯亮起时间除以每个循环的总时间即可得;(2)将绿灯亮起的时间划分为第1个20秒和第2个20秒,记作绿1、绿2 , 画出树状图列出所有等可能结果,根据概率公式求解可得.
【考点精析】根据题目的已知条件,利用列表法与树状图法的相关知识可以得到问题的答案,需要掌握当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,直线AB和CD交于点O,OE⊥AB,垂足为点O,OP平分∠EOD,∠AOD=144°.
(1)求∠AOC与∠COE的度数;
(2)求∠BOP的度数.

【答案】(1)∠AOC=36°,∠COE=54°,(2)∠BOP=27°.
【解析】
(1)由邻补角定义,可求得得∠AOC度数,由垂直定义,可得∠AOE=∠BOE=90°,由余角定义可求得∠COE;
(2)由邻补角定义可得∠DOE度数,由OO平分∠DOE,可得∠EOP度数,再由余角定义可求得∠BOP度数.
(1)∵∠AOC+∠AOD=180°,∠AOD=144°,
∴∠AOC=180°-∠AOD=180°-144°=36°,
∵OE⊥AB,
∴∠AOE=∠BOE=90°,
∴∠COE=∠AOE-∠AOC=90°-36°=54°,
(2)∵∠COE+∠DOE=180°,
∴∠DOE=180°-∠COE=180°-54°=126°,
∵OO平分∠DOE,
∴∠EOP=![]() ∠DOE=
∠DOE=![]() ×126°=63°,
×126°=63°,
∴∠BOP=∠BOE-∠EOP=90°-63°=27°.
【点睛】
本题考查了对顶角、邻补角以及垂线的性质,是基础知识要熟练掌握.
【题型】解答题
【结束】
27
【题目】如表为某市居民每月用水收费标准,(单位:元/m3).
用水量 | 单价 |
0<x≤20 | a |
剩余部分 | a+1.1 |
(1)某用户1月用水10立方米,共交水费26元,则a= 元/m3;
(2)在(1)的条件下,若该用户2月用水25立方米,则需交水费 元;
(3)在(1)的条件下,若该用户水表3月份出了故障,只有70%的用水量记入水表中,该用户3月份交了水费81.6元.请问该用户实际用水多少立方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一段街道的两边缘所在直线分别为AB, PQ,并且AB∥PQ.建筑物的一端DE所在的直线MN⊥AB于点M,交PQ于点N,步行街宽MN为13.4米,建筑物宽DE为6米,光明巷宽EN为2.4米.小亮在胜利街的A处,测得此时AM为12米,求此时小亮距建筑物拐角D处有多远?
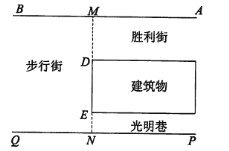
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提倡全民健身活动, 某社区准备购买羽毛球和羽毛球拍供社区居民使用, 某体育用品商店羽毛球每盒 10 元, 羽毛球拍每副 40 元 .该商店有两种优惠方案,方案一: 不购买会员卡时, 羽毛球享受 8.5 折优惠, 羽毛球拍购买 5 副(含5 副) 以上才能享受 8.5 折优惠, 5 副以下必须按定价购买;方案二: 每张会员卡 20 元, 办理会员卡时, 全部商品享受 8 折优惠 . 设该社区准备购买羽毛球拍 6 副, 羽毛球![]() 盒, 请回答下列问题:
盒, 请回答下列问题:
(1)如果一位体育爱好者按方案一只购买了 4 副羽毛球拍,求他购买时所需要的费用;
(2)用含![]() 的代数式分别表示该社区按方案一和方案二购买所需要的钱数;
的代数式分别表示该社区按方案一和方案二购买所需要的钱数;
(3)①直接写出一个![]() 的值, 使方案一比方案二优惠;
的值, 使方案一比方案二优惠;
②直接写出一个![]() 的值, 使方案二比方案一优惠 .
的值, 使方案二比方案一优惠 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知正方形ABCD,直角三角形纸板的一个锐角顶点与点A重合,纸板绕点A旋转时,直角三角形纸板的一边与直线CD交于E,分别过B、D作直线AE的垂线,垂足分别为F、G. 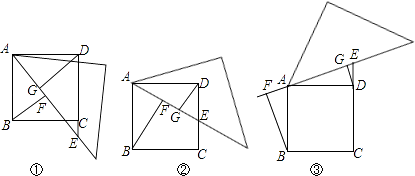
(1)当点E在DC延长线时,如图①,求证:BF=DG﹣FG;
(2)将图①中的三角板绕点A逆时针旋转得图②、图③,此时BF、FG、DG之间又有怎样的数量关系?请直接写出结论(不必证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,对角线AD,BC交于点O,点E、F分别在AC,CD边上,EF∥AD,交BC于点P,若点O是△BEF的重心.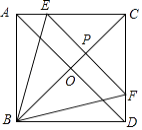
(1)求tan∠ABE的值.
(2)求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了深化课程改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“科学实验”、“音乐舞蹈”和“手工编织”等多个社团,要求每位学生都自主选择其中一个社团.为此,随机调查了本校各年级部分学生选择社团的意向,并将调查结果绘制成如下统计图表(不完整):
选择意向 | 所占百分比 |
文学鉴赏 | a |
科学实验 | 35% |
音乐舞蹈 | b |
手工编织 | 10% |
其他 | c |
根据统计图表中的信息,解答下列问题: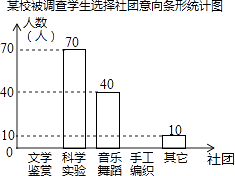
(1)本次调查的学生总人数为;
(2)补全条形统计图;
(3)将调查结果绘成扇形统计图,则“音乐舞蹈”社团所在扇形所对应的圆心角为;
(4)若该校共有1200名学生,试估计全校选择“科学实验”社团的学生人数为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com