
【题目】甲,乙两辆汽车先后从A地出发到B地,甲车出发1小时后,乙车才出发,如图所示的l1和l2表示甲,乙两车相对于出发地的距离y(km)与追赶时间x(h)之间的关系:
(1)哪条线表示乙车离出发地的距离y与追赶时间x之间的关系?
(2)甲,乙两车的速度分别是多少?
(3)试分别确定甲,乙两车相对于出发地的距离y(km)与追赶时间x(h)之间的关系式;
(4)乙车能在1.5小时内追上甲车吗?若能,说明理由;若不能,求乙车出发几小时才能追上甲?

【答案】(1)l2表示乙车离出发地的距离y与追赶时间x之间的关系;(2)甲车的速度为60km/h,乙车的速度为90km/h;(3)y1=60x+60;y2=90x;(4)乙车不能在1.5小时内追上甲车.乙车追上甲车时,乙车行驶了2小时.
【解析】
(1)通过分析函数图象就可以得出l2表示B车离出发地的距离y与追赶时间x之间的关系;
(2)根据速度=路程÷时间就可以求出两车的速度;
(3)根据题意得出函数关系式即可;
(4)设B车行驶a小时可以追上A车,由追击问题的等量关系建立方程求出其解;
(1)由函数图象,得
l2表示乙车离出发地的距离y与追赶时间x之间的关系;
(2)甲车的速度为![]() =60km/h,乙车的速度为
=60km/h,乙车的速度为![]() =90km/h;
=90km/h;
(3)甲车的函数的关系式为:y1=60x+60;
乙车的函数关系式为:y2=90x;
(4)设乙车行驶a小时可以追上甲车,由题意,得
90a=60+60a,
解得:a=2,
∵1.5<2,
∴乙车不能在1.5小时内追上甲车,乙车追上甲车时,乙车行驶了2小时.


科目:初中数学 来源: 题型:
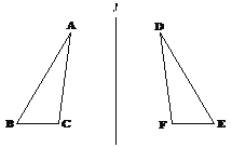
【题目】如图所示,是用笔尖扎重叠的纸得到的成轴对称的图案,请根据图形写出:
(1)两组对应点:__________和__________;
(2)两组对应线段:__________和__________;
(3)两组对应角:__________和__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知下列命题: ①同位角相等;
②若a>b>0,则 ![]() ;
;
③对角线相等且互相垂直的四边形是正方形;
④抛物线y=x2﹣2x与坐标轴有3个不同交点;
⑤边长相等的多边形内角都相等.
其中正确的命题有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将OA2B2变换成△OA3B3;已知变换过程中各点坐标分别为A(1,3),A1(2,3),A2(4,3),A3(8,3),B(2,0),B1(4,0),B2(8,0),B3(16,0).
(1)观察每次变换前后的三角形有何变化,找出规律,按此规律再将△OA3B3变换成△OA4B4,则A4的坐标为 ,B4的坐标为 .
(2)按以上规律将△OAB进行n次变换得到△OAnBn,则An的坐标为 ,Bn的坐标为 ;
(3)△OAnBn的面积为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中有一正方形AOBC,反比例函数 ![]() 经过正方形AOBC对角线的交点,半径为(4﹣2
经过正方形AOBC对角线的交点,半径为(4﹣2 ![]() )的圆内切于△ABC,则k的值为 .
)的圆内切于△ABC,则k的值为 . 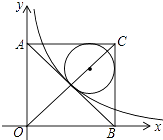
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2+bx+c与x轴交于点A(1,0)和点B,与y轴交于点C(0,﹣3).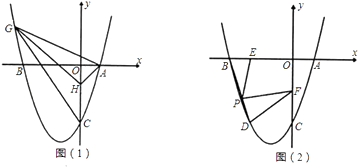
(1)求抛物线的解析式;
(2)如图(1),己知点H(0,﹣1).问在抛物线上是否存在点G (点G在y轴的左侧),使得S△GHC=S△GHA?若存在,求出点G的坐标;若不存在,请说明理由;
(3)如图(2),抛物线上点D在x轴上的正投影为点E(﹣2,0),F是OC的中点,连接DF,P为线段BD上的一点,若∠EPF=∠BDF,求线段PE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,DE是边AB的垂直平分线,交AB于E、交AC于D,连接BD.
(1)若∠ABC=∠C,∠A=40°,求∠DBC的度数;
(2)若AB=AC,且△BCD的周长为18cm,△ABC的周长为30cm,求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=13,BC=14.
(1)如图1,AD⊥BC于点D,且BD=5,则△ABC的面积为 ;
(2)在(1)的条件下,如图2,点H是线段AC上任意一点,分别过点A,C作直线BH的垂线,垂足为E,F,设BH=x,AE=m,CF=n,请用含x的代数式表示m+n,并求m+n的最大值和最小值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com