
【题目】如图,在平面直角坐标系中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将OA2B2变换成△OA3B3;已知变换过程中各点坐标分别为A(1,3),A1(2,3),A2(4,3),A3(8,3),B(2,0),B1(4,0),B2(8,0),B3(16,0).
(1)观察每次变换前后的三角形有何变化,找出规律,按此规律再将△OA3B3变换成△OA4B4,则A4的坐标为 ,B4的坐标为 .
(2)按以上规律将△OAB进行n次变换得到△OAnBn,则An的坐标为 ,Bn的坐标为 ;
(3)△OAnBn的面积为 .

【答案】(1)点A4的坐标为(16,3),点B4的坐标为(32,0);(2)An的坐标为(2n,3),Bn的坐标为(2n+1,0);(3)△OAnBn的面积为3×2n.
【解析】
(1)根据题目中的信息可以发现A1、A2、A3各点坐标的关系为横坐标是2n,纵坐标都是3,故可求得A4的坐标;B1、B2、B3各点的坐标的关系为横坐标是2n+1,纵坐标都为0,从而可求得点B4的坐标.
(2)根据(1)中发现的规律可以求得An、Bn点的坐标;
(3)依据An、Bn点的坐标,利用三角形面积计算公式,即可得到结论.
(1)∵A1(2,3)、A2(4,3)、A3(8,3),
∴A4的横坐标为:24=16,纵坐标为:3,
故点A4的坐标为:(16,3);
又∵B1(4,0)、B2(8,0)、B3(16,0),
∴B4的横坐标为:25=32,纵坐标为:0,
故点B4的坐标为:(32,0);
(2)由A1(2,3)、A2(4,3)、A3(8,3),可以发现它们各点坐标的关系为横坐标是2n,纵坐标都是3.
故An的坐标为:(2n,3);
由B1(4,0)、B2(8,0)、B3(16,0),可以发现它们各点坐标的关系为横坐标是2n+1,纵坐标都是0,
故Bn的坐标为:(2n+1,0);
(3)∵An的坐标为:(2n,3),Bn的坐标为:(2n+1,0),
∴△OAnBn的面积为![]() ×2n+1×3=3×2n.
×2n+1×3=3×2n.


 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:
【题目】平安加气站某日8:00的储气量为10 000立方米.从8:00开始,3把加气枪同时以每车20立方米的加气量,依次给在加气站排队等候的若干辆车加气.8:30时,为缓解排队压力,又增开了2把加气枪.假设加气过程中每把加气枪加气的速度是匀速的,在不关闭加气枪的情况下,加气站的储气量![]() (立方米)与时间
(立方米)与时间![]() (小时)之间的函数关系如图中的折线
(小时)之间的函数关系如图中的折线![]() 所示.
所示.
(1)分别求出8:00 ~8:30及8:30之后加气站的储气量![]() (立方米)与时间
(立方米)与时间![]() (小时)之间的函数表达式.
(小时)之间的函数表达式.
(2)前30辆车能否在当天8:42之前加完气?
(3)若前![]() 辆车按上述方式加气,它们加完气的时间要比不增开加气枪加完气的时间提前1个小时,求
辆车按上述方式加气,它们加完气的时间要比不增开加气枪加完气的时间提前1个小时,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2012年6月5日是“世界环境日”,南宁市某校举行了“绿色家园”演讲比赛,赛后整理参赛同学的成绩,制作成直方图(如图). 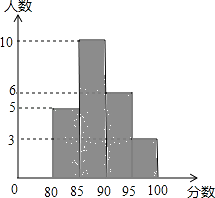
(1)分数段在范围的人数最多;
(2)全校共有多少人参加比赛?
(3)学校决定选派本次比赛成绩最好的3人参加南宁市中学生环保演讲决赛,并为参赛选手准备了红、蓝、白颜色的上衣各1件和2条白色、1条蓝色的裤子.请用“列表法”或“树形图法”表示上衣和裤子搭配的所有可能出现的结果,并求出上衣和能搭配成同一种颜色的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有红、白两种颜色的小球,这些球除颜色外都相同,其中红球有2个,若从中随机摸出一个球,这个球是白球的概率为 ![]() .
.
(1)求袋子中白球的个数;(请通过列式或列方程解答)
(2)随机摸出一个球后,放回并搅匀,再随机摸出一个球,求两次都摸到相同颜色的小球的概率.(请结合树状图或列表解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠CAB=30°,AB=10,点D在线段AB上,AD=2.点P,Q以相同的速度从D点同时出发,点P沿DB方向运动,点Q沿DA方向到点A后立刻以原速返回向点B运动.以PQ为直径构造⊙O,过点P作⊙O的切线交折线AC﹣CB于点E,将线段EP绕点E顺时针旋转60°得到EF,过F作FG⊥EP于G,当P运动到点B时,Q也停止运动,设DP=m. 
(1)当2<m≤8时,AP=,AQ=.(用m的代数式表示)
(2)当线段FG长度达到最大时,求m的值;
(3)在点P,Q整个运动过程中, ①当m为何值时,⊙O与△ABC的一边相切?
②直接写出点F所经过的路径长是.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲,乙两辆汽车先后从A地出发到B地,甲车出发1小时后,乙车才出发,如图所示的l1和l2表示甲,乙两车相对于出发地的距离y(km)与追赶时间x(h)之间的关系:
(1)哪条线表示乙车离出发地的距离y与追赶时间x之间的关系?
(2)甲,乙两车的速度分别是多少?
(3)试分别确定甲,乙两车相对于出发地的距离y(km)与追赶时间x(h)之间的关系式;
(4)乙车能在1.5小时内追上甲车吗?若能,说明理由;若不能,求乙车出发几小时才能追上甲?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有红、白两种颜色的小球(除颜色外其余都相同),其中红球3个,白球1个.
(1)求任意摸出一球是白球的概率;
(2)甲同学先随机摸出一个小球(不放回),再随机摸出一个小球,请用画树状图或列表的方法求两次摸出都是红球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在边长为5的菱形ABCD中,cos∠BAD= ![]() ,点E是射线AB上的点,作EF⊥AB,交AC于点F.
,点E是射线AB上的点,作EF⊥AB,交AC于点F. 
(1)求菱形ABCD的面积;
(2)求证:AE=2EF;
(3)如图2,过点F,E,B作⊙O,连结DF,若⊙O与△CDF的边所在直线相切,求所有满足条件的AE的长度. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com