
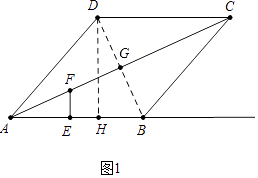
【题目】如图1,在边长为5的菱形ABCD中,cos∠BAD= ![]() ,点E是射线AB上的点,作EF⊥AB,交AC于点F.
,点E是射线AB上的点,作EF⊥AB,交AC于点F. 
(1)求菱形ABCD的面积;
(2)求证:AE=2EF;
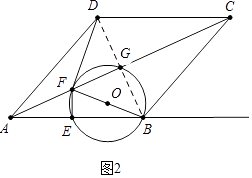
(3)如图2,过点F,E,B作⊙O,连结DF,若⊙O与△CDF的边所在直线相切,求所有满足条件的AE的长度. 
【答案】
(1)解:如图1中,作DH⊥AB于H.
在Rt△ADH中,∵∠AHD=90°,AD=5,cos∠DAH= ![]() ,
,
∴AH=3,DH= ![]() =4,
=4,
∴S菱形ABCD=ABDH=5×4=20.
(2)解:证明:如图1中,BD与AC交于点G.
在Rt△DHB中,∵DH=4,BH=2,
∴BD= ![]() =
= ![]() =2
=2 ![]() ,
,
∵四边形ABCD是菱形,
∴AC⊥BD,BG=DG= ![]() ,AG=
,AG= ![]() =
= ![]() =2
=2 ![]() ,
,
∵∠EAF=∠BAG,∠AEF=∠AGB=90°,
∴△AEF∽△AGB,
∴ ![]() =
= ![]() =
= ![]() =2,
=2,
∴AE=2EF.
(3)解:①如图2中,当⊙O与直线DF相切时,易知,∠BFD=90°,DF=BF.
∵BD=2 ![]() ,
,
∴BF= ![]() ,设EF=x,则AE=2EF=2x,
,设EF=x,则AE=2EF=2x,
在Rt△BEF中,∵BF2=EF2+BE2,
∴10=x2+(5﹣2x)2,
解得x=1或3,
∴AE=2或6时,⊙O与直线DF相切.
②如图3中,当⊙O与AC相切时,易知点F与G重合,设EF=x,AE=2x,
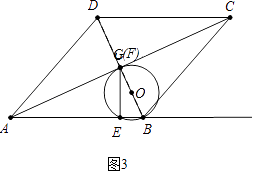
在Rt△AFE中,∵AG2=AE2+GE2,
∴20=4x2+x2,
∴x2=4,
∴x=2,
∴AE=4时,⊙O与直线CF相切.
③如图4中,当⊙O与CD相切于点M,延长MO交AE与H,设EF=x,则AE=2x,则OH= ![]() EF=
EF= ![]() x,BF=
x,BF= ![]() ,
,
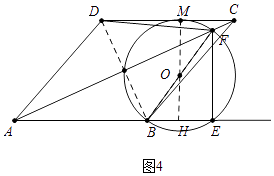
∵HM=4,
∴OM+OH=4,
∴ ![]() +
+ ![]() x=4,
x=4,
整理得,4x2﹣4x﹣39=0,
解得x= ![]() 或
或 ![]() (舍弃),
(舍弃),
∴AE=1+2 ![]() ,
,
综上所述,满足条件的AE的值为2或4或6或1+2 ![]() .
.
【解析】(1)如图1中,作DH⊥AB于H.在Rt△ADH中,由∠AHD=90°,AD=5,cos∠DAH= ![]() ,推出AH=3,DH=
,推出AH=3,DH= ![]() =4,即可解决问题;(2)如图1中,BD与AC交于点G.在Rt△DHB中,可得BD=
=4,即可解决问题;(2)如图1中,BD与AC交于点G.在Rt△DHB中,可得BD= ![]() =
= ![]() =2
=2 ![]() ,由四边形ABCD是菱形,推出AC⊥BD,BG=DG=
,由四边形ABCD是菱形,推出AC⊥BD,BG=DG= ![]() ,AG=
,AG= ![]() =
= ![]() =2
=2 ![]() ,由△AEF∽△AGB,推出
,由△AEF∽△AGB,推出 ![]() =
= ![]() =
= ![]() =2,即可解决问题;(3)分三种情形分别求解:①如图2中,当⊙O与直线DF相切时.②如图3中,当⊙O与AC相切时.③如图4中,当⊙O与CD相切于点M.分别求解即可;
=2,即可解决问题;(3)分三种情形分别求解:①如图2中,当⊙O与直线DF相切时.②如图3中,当⊙O与AC相切时.③如图4中,当⊙O与CD相切于点M.分别求解即可;


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将OA2B2变换成△OA3B3;已知变换过程中各点坐标分别为A(1,3),A1(2,3),A2(4,3),A3(8,3),B(2,0),B1(4,0),B2(8,0),B3(16,0).
(1)观察每次变换前后的三角形有何变化,找出规律,按此规律再将△OA3B3变换成△OA4B4,则A4的坐标为 ,B4的坐标为 .
(2)按以上规律将△OAB进行n次变换得到△OAnBn,则An的坐标为 ,Bn的坐标为 ;
(3)△OAnBn的面积为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,DE是边AB的垂直平分线,交AB于E、交AC于D,连接BD.
(1)若∠ABC=∠C,∠A=40°,求∠DBC的度数;
(2)若AB=AC,且△BCD的周长为18cm,△ABC的周长为30cm,求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+4A(1,﹣1),B(5,﹣1),与y轴交于点C. 
(1)求抛物线的函数表达式;
(2)如图1,连接CB,若点P在直线BC上方的抛物线上,△BCP的面积为15,求点P的坐标;
(3)如图2,⊙O1过点A、B、C三点,AE为直径,点M为弧ACE上的一动点(不与点A,E重合),∠MBN为直角,边BN与ME的延长线交于N,求线段BN长度的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据要求完成下列题目:
(1)图中有_____块小正方体;
(2)请在下面方格纸中分别画出它的主视图、左视图和俯视图;
(3)用小正方体搭一几何体,使得它的俯视图和左视图与你在图方格中所画的图一致,若这样的几何体最少要m个小正方体,最多要n个小正方体,则m+n的值为____.

【答案】(1)7;(2)画图见解析;(3)16
【解析】
(1)直接根据立体图形得出小正方体的个数;
(2)主视图从左往右小正方形的个数为1,3,2;左视图从左往右小正方形的个数为3,1;俯视图从左往右小正方形的个数1,2,1;
(3)由俯视图易得最底层小立方块的个数,由左视图找到其余层数里最少个数和最多个数相加即可.
(1)图中有7块小正方体;
故答案为:7;
(2)如图所示:
 ;
;
(3)用小立方体搭一几何体,使得它的俯视图和左视图与你在上图方格中所画的图一致,则这样的几何体最少要6个小立方块,最多要10个小立方块.则m+n=16
故答案为:16
【点睛】
此题主要考查了三视图,用到的知识点为:三视图分为主视图、左视图、俯视图,分别是从物体正面、左面和上面看,所得到的图形;俯视图决定底层立方块的个数,易错点是由主视图得到其余层数里最少的立方块个数和最多的立方块个数.
【题型】解答题
【结束】
24
【题目】如图,点P是∠AOB的边OA上的一点,作∠AOB的平分线ON;
(1)过点P画OB的平行线交ON于点M;
(2)过点M画OB的垂线,垂足为H;
(3)度量线段PO、PM与MH的长度,会发现:线段PO与PM的大小关系是 ;线段MH与PM的大小关系是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=13,BC=14.
(1)如图1,AD⊥BC于点D,且BD=5,则△ABC的面积为 ;
(2)在(1)的条件下,如图2,点H是线段AC上任意一点,分别过点A,C作直线BH的垂线,垂足为E,F,设BH=x,AE=m,CF=n,请用含x的代数式表示m+n,并求m+n的最大值和最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作:
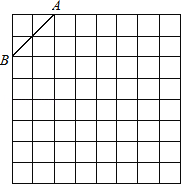
(1)在网格中建立平面直角坐标系,使A点坐标为(﹣2,4),B点坐标为(﹣4,2);
(2)在第二象限内的格点上画一点C,使点C与线段AB组成一个以AB为底的等腰三角形,且腰长是无理数,则C点坐标是________;
(3)△ABC的周长=_________(结果保留根号);
(4)画出△ABC关于关于y轴对称的△A′B′C′.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com