
【题目】(9分)如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作:
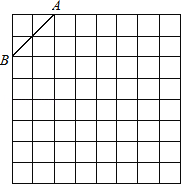
(1)在网格中建立平面直角坐标系,使A点坐标为(﹣2,4),B点坐标为(﹣4,2);
(2)在第二象限内的格点上画一点C,使点C与线段AB组成一个以AB为底的等腰三角形,且腰长是无理数,则C点坐标是________;
(3)△ABC的周长=_________(结果保留根号);
(4)画出△ABC关于关于y轴对称的△A′B′C′.
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:初中数学 来源: 题型:
【题目】如图1,在边长为5的菱形ABCD中,cos∠BAD= ![]() ,点E是射线AB上的点,作EF⊥AB,交AC于点F.
,点E是射线AB上的点,作EF⊥AB,交AC于点F. 
(1)求菱形ABCD的面积;
(2)求证:AE=2EF;
(3)如图2,过点F,E,B作⊙O,连结DF,若⊙O与△CDF的边所在直线相切,求所有满足条件的AE的长度. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,圆D与y轴相切于点C(0,4),与x轴相交于A、B两点,且AB=6.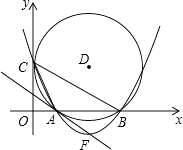
(1)则D点的坐标是 ( , ),圆的半径为;
(2)sin∠ACB=;经过C、A、B三点的抛物线的解析式;
(3)设抛物线的顶点为F,证明直线FA与圆D相切;
(4)在x轴下方的抛物线上,是否存在一点N,使△CBN面积最大,最大值是多少,并求出N点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一段街道的两边缘所在直线分别为AB, PQ,并且AB∥PQ.建筑物的一端DE所在的直线MN⊥AB于点M,交PQ于点N,步行街宽MN为13.4米,建筑物宽DE为6米,光明巷宽EN为2.4米.小亮在胜利街的A处,测得此时AM为12米,求此时小亮距建筑物拐角D处有多远?
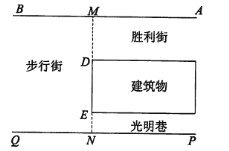
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提倡全民健身活动, 某社区准备购买羽毛球和羽毛球拍供社区居民使用, 某体育用品商店羽毛球每盒 10 元, 羽毛球拍每副 40 元 .该商店有两种优惠方案,方案一: 不购买会员卡时, 羽毛球享受 8.5 折优惠, 羽毛球拍购买 5 副(含5 副) 以上才能享受 8.5 折优惠, 5 副以下必须按定价购买;方案二: 每张会员卡 20 元, 办理会员卡时, 全部商品享受 8 折优惠 . 设该社区准备购买羽毛球拍 6 副, 羽毛球![]() 盒, 请回答下列问题:
盒, 请回答下列问题:
(1)如果一位体育爱好者按方案一只购买了 4 副羽毛球拍,求他购买时所需要的费用;
(2)用含![]() 的代数式分别表示该社区按方案一和方案二购买所需要的钱数;
的代数式分别表示该社区按方案一和方案二购买所需要的钱数;
(3)①直接写出一个![]() 的值, 使方案一比方案二优惠;
的值, 使方案一比方案二优惠;
②直接写出一个![]() 的值, 使方案二比方案一优惠 .
的值, 使方案二比方案一优惠 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知正方形ABCD,直角三角形纸板的一个锐角顶点与点A重合,纸板绕点A旋转时,直角三角形纸板的一边与直线CD交于E,分别过B、D作直线AE的垂线,垂足分别为F、G. 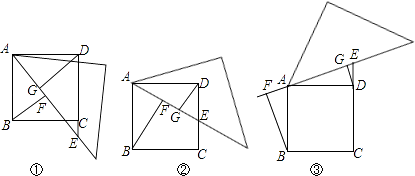
(1)当点E在DC延长线时,如图①,求证:BF=DG﹣FG;
(2)将图①中的三角板绕点A逆时针旋转得图②、图③,此时BF、FG、DG之间又有怎样的数量关系?请直接写出结论(不必证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学九(1)班为了了解全班学生喜欢球类活动的情况,采取全面调查的方法,从足球、乒乓球、篮球、排球等四个方面调查了全班学生的兴趣爱好,根据调查的结果组建了4个兴趣小组,并绘制成如图所示的两幅不完整的统计图(如图①,②,要求每位学生只能选择一种自己喜欢的球类),请你根据图中提供的信息解答下列问题: 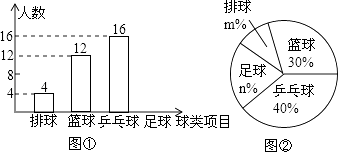
(1)九(1)班的学生人数为 , 并把条形统计图补充完整;
(2)扇形统计图中m= , n= , 表示“足球”的扇形的圆心角是度;
(3)排球兴趣小组4名学生中有3男1女,现在打算从中随机选出2名学生参加学校的排球队,请用列表或画树状图的方法求选出的2名学生恰好是1男1女的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com