
【题目】如图,在平面直角坐标系中,圆D与y轴相切于点C(0,4),与x轴相交于A、B两点,且AB=6.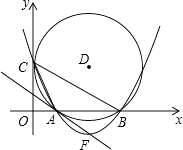
(1)则D点的坐标是 ( , ),圆的半径为;
(2)sin∠ACB=;经过C、A、B三点的抛物线的解析式;
(3)设抛物线的顶点为F,证明直线FA与圆D相切;
(4)在x轴下方的抛物线上,是否存在一点N,使△CBN面积最大,最大值是多少,并求出N点坐标.
【答案】
(1)5;4;5
(2)![]() ;y=
;y= ![]() x2﹣
x2﹣ ![]() x+4
x+4
(3)
证明:因为D为圆心,A在圆周上,DA=r=5,故只需证明∠DAF=90°,
抛物线顶点坐标:F(5,﹣ ![]() ),DF=4+
),DF=4+ ![]() =
= ![]() ,AF=
,AF= ![]() =
= ![]() ,
,
∵DA2+AF2=52+( ![]() )2=
)2= ![]() =(
=( ![]() )2=DF2,
)2=DF2,
∴∠DAF=90°
所以AF切于圆D
(4)
解:存在点N,使△CBN面积最大.
根据点B及点C的坐标可得:直线BC的解析式为:y=﹣ ![]() x+4,
x+4,
设N点坐标(a, ![]() ),过点N作NP与y轴平行,交BC于点P,
),过点N作NP与y轴平行,交BC于点P,
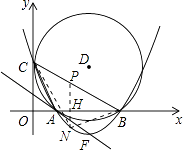
可得P点坐标为(a, ![]() ),
),
则NP= ![]() ﹣(
﹣( ![]() )=
)= ![]()
故S△BCN=S△BPN+S△PCN= ![]() ×PN×OH+
×PN×OH+ ![]() ×PN×BH=
×PN×BH= ![]() PN×BO=
PN×BO= ![]() ×8×(
×8×( ![]() )=16﹣(a﹣4)2
)=16﹣(a﹣4)2
当a=4时,S△BCN最大,最大值为16,此时,N(4,﹣2)
【解析】(1)解:连接DC,则DC⊥y轴,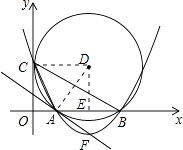
过点D作DE⊥AB于点E,则DE垂直平分AB,
∵AB=6,
∴AE=3,
在Rt△ADE中,AD= ![]() =
= ![]() =5,
=5,
故可得点D的坐标为(5,4),圆的半径为5;
·(2)解:在Rt△AOC中,AC= ![]() =
= ![]() =2
=2 ![]() ,
,
在Rt△BOC中,BC= ![]() =
= ![]() =4
=4 ![]() ,
,
∵S△ABC= ![]() AC×BCsin∠ACB=
AC×BCsin∠ACB= ![]() AB×CO,
AB×CO,
∴sin∠ACB= ![]() =
= ![]() ;
;
设经过点A、B、C三点的抛物线解析式为:y=ax2+bx+c,
将三点坐标代入可得: 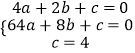 ,
,
解得: 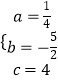 ,
,
故经过C、A、B三点的抛物线的解析式为:y= ![]() x2﹣
x2﹣ ![]() x+4.
x+4.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,DE是边AB的垂直平分线,交AB于E、交AC于D,连接BD.
(1)若∠ABC=∠C,∠A=40°,求∠DBC的度数;
(2)若AB=AC,且△BCD的周长为18cm,△ABC的周长为30cm,求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=13,BC=14.
(1)如图1,AD⊥BC于点D,且BD=5,则△ABC的面积为 ;
(2)在(1)的条件下,如图2,点H是线段AC上任意一点,分别过点A,C作直线BH的垂线,垂足为E,F,设BH=x,AE=m,CF=n,请用含x的代数式表示m+n,并求m+n的最大值和最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
为了缓解北京市西部地区的交通拥堵现象,市政府决定修建本市的第一条磁浮地铁线路﹣﹣“S1线”.该线路连接北京城区与门头沟,西起石门营,向东经苹果园,终点至慈寿寺与6号线和10号线相接.为使该工程提前4个月完成,在保证质量的前提下,必须把工作效率提高10%.问原计划完成这项工程需用多少个月.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,A、B在数轴上对应的数分别用a、b表示,且(a﹣20)2+|b+10|=0,P是数轴上的一个动点.
(1)在数轴上标出A、B的位置,并求出A、B之间的距离;
(2)已知线段OB上有点C且|BC|=6,当数轴上有点P满足PB=2PC时,求P点对应的数;
(3)动点P从原点开始第一次向左移动1个单位长度,第二次向右移动3个单位长度,第三次向左移动5个单位长度,第四次向右移动7个单位长度,…….点P能移动到与A或B重合的位置吗?若不能,请直接回答;若能,请直接指出,第几次移动,与哪一点重合.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了能以“更新、更绿、更洁、更宁”的城市形象迎接2011年大运会的召开,深圳市全面实施市容市貌环境提升行动.某工程队承担了一段长为1500米的道路绿化工程,施工时有两张绿化方案: 甲方案是绿化1米的道路需要A型花2枝和B型花3枝,成本是22元;
乙方案是绿化1米的道路需要A型花1枝和B型花5枝,成本是25元.
现要求按照乙方案绿化道路的总长度不能少于按甲方案绿化道路的总长度的2倍.
(1)求A型花和B型花每枝的成本分别是多少元?
(2)求当按甲方案绿化的道路总长度为多少米时,所需工程的总成本最少?总成本最少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作:
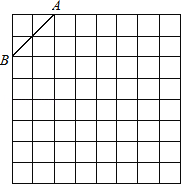
(1)在网格中建立平面直角坐标系,使A点坐标为(﹣2,4),B点坐标为(﹣4,2);
(2)在第二象限内的格点上画一点C,使点C与线段AB组成一个以AB为底的等腰三角形,且腰长是无理数,则C点坐标是________;
(3)△ABC的周长=_________(结果保留根号);
(4)画出△ABC关于关于y轴对称的△A′B′C′.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若BM+CN=9,则线段MN的长为( ) 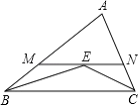
A.6
B.7
C.8
D.9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com