
����Ŀ��Ϊ�����ԡ����¡����̡����ࡢ�������ij�������ӭ��2011����˻���ٿ���������ȫ��ʵʩ������ò���������ж���ij���̶ӳе���һ�γ�Ϊ1500�ĵ�·�̻����̣�ʩ��ʱ�������̻������� �������̻�1�ĵ�·��ҪA�ͻ�2֦��B�ͻ�3֦���ɱ���22Ԫ��
�ҷ������̻�1�ĵ�·��ҪA�ͻ�1֦��B�ͻ�5֦���ɱ���25Ԫ��
��Ҫ�����ҷ����̻���·���ܳ��Ȳ������ڰ������̻���·���ܳ��ȵ�2����
��1����A�ͻ���B�ͻ�ÿ֦�ijɱ��ֱ��Ƕ���Ԫ��
��2���������̻��ĵ�·�ܳ���Ϊ������ʱ�����蹤�̵��ܳɱ����٣��ܳɱ������Ƕ���Ԫ��
���𰸡�
��1���⣺��A�ͻ���B�ͻ�ÿ֦�ijɱ��ֱ���xԪ��yԪ����������ã�
![]()
��ã� ![]()
����A�ͻ���B�ͻ�ÿ֦�ijɱ��ֱ���5Ԫ��4Ԫ
��2���⣺�谴�����̻��ĵ�·�ܳ���Ϊa�ף���������ã�
1500��a��2a
a��500
�����蹤�̵��ܳɱ���
5��2a+4��3a+5��1500��a��+4��5��1500��a��
=10a+12a+7500��5a+30000��20a
=37500��3a
�൱�������̻��ĵ�·�ܳ���Ϊ500��ʱ�����蹤�̵��ܳɱ�����
w=37500��3��500
=36000��Ԫ��
�൱�������̻��ĵ�·�ܳ���Ϊ500��ʱ�����蹤�̵��ܳɱ����٣��ܳɱ�������36000Ԫ
����������1�����������������A�ͻ���B�ͻ�ÿ֦�ijɱ��ֱ���xԪ��yԪ�����������г������飬�������A�ͻ���B�ͻ�ÿ֦�ijɱ�����2���������ȸ��������谴�����̻��ĵ�·�ܳ���Ϊa�ף����������г�����ʽ������������������̵��ܳɱ����ɵó��𰸣�


 �����������Ů��ͯ������ϵ�д�
�����������Ů��ͯ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ڡ�OAB�У���OAB=90�㣬��AOB=30�㣬OB=8����OBΪ�ߣ��ڡ�OAB�����ȱߡ�OBC��D��OB���е㣬����AD���ӳ���OC��E�� 
��1����֤���ı���ABCE��ƽ���ı��Σ�
��2����ͼ2����ͼ1�е��ı���ABCO�۵���ʹ��C���A�غϣ��ۺ�ΪFG����OG�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����22�׳�����ʺ�6�׳���ΧǽΧ��һ�����μ��ᣮ
��1���ְֵķ����ǣ�һ����ǽ��������������ʣ���ְ�Χ�ɵļ����������Ƕ��٣�
��2��С���ķ����ǣ�����ǽ��һ������ʼӳ���Ϊһ�ߣ���������Ҳ����ʣ�ҪʹΧ�ɵļ�������������ǽ��һ��Ӧ���ټӳ����׳�����ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ԲD��y�������ڵ�C��0��4������x���ཻ��A��B���㣬��AB=6��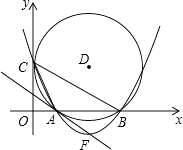
��1����D��������� �� �� ����Բ�İ뾶Ϊ��
��2��sin��ACB=������C��A��B����������ߵĽ���ʽ��
��3���������ߵĶ���ΪF��֤��ֱ��FA��ԲD���У�
��4����x���·����������ϣ��Ƿ����һ��N��ʹ��CBN���������ֵ�Ƕ��٣������N�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧϰС������ͬѧ����ĩģ�⿼�ԣ�����Ϊ120���ijɼ����£�100��100��x��x��80����֪�������ݵ���λ����ƽ������ȣ���ô����x��ֵ������_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
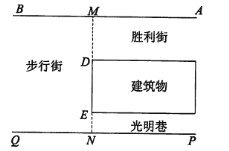
����Ŀ����ͼ��ʾ��һ�νֵ�������Ե����ֱ�߷ֱ�ΪAB�� PQ������AB��PQ.�������һ��DE���ڵ�ֱ��MN��AB�ڵ�M����PQ�ڵ�N�����нֿ�MNΪ13.4�ף��������DEΪ6�ף��������ENΪ2.4��.С����ʤ���ֵ�A������ô�ʱAMΪ12�ף����ʱС���ཨ����ս�D���ж�Զ?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AB=4��AD=2����E��F���Խ���AC�ϣ���AE=EF=FC�����߶�BE��DF�ľ���Ϊ�� �� 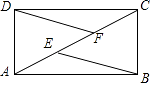
A.![]()
B.1
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����֪������ABCD��ֱ��������ֽ���һ����Ƕ������A�غϣ�ֽ���Ƶ�A��תʱ��ֱ��������ֽ���һ����ֱ��CD����E���ֱ��B��D��ֱ��AE�Ĵ��ߣ�����ֱ�ΪF��G�� 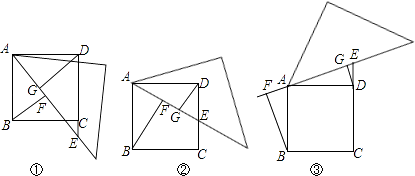
��1������E��DC�ӳ���ʱ����ͼ�٣���֤��BF=DG��FG��
��2����ͼ���е����ǰ��Ƶ�A��ʱ����ת��ͼ�ڡ�ͼ�ۣ���ʱBF��FG��DG֮������������������ϵ����ֱ��д�����ۣ�����֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ����֪��1=��2����3=��4����֤��AC��DF��BC��EF.֤���������£�
�ߡ�1=��2����֪����
��AC��DF��A��ͬλ����ȣ���ֱ��ƽ�У���
���3=��5��B���ڴ�����ȣ���ֱ��ƽ�У���
���ߡ�3=��4����֪��
���5=��4��C��������������
��BC��EF��D���ڴ�����ȣ���ֱ��ƽ�У���
�����������ж����ݴ�����ǣ� ��
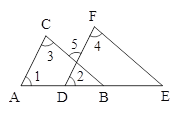
A. A B. B C. C D. D
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com