
【题目】在如图,已知∠1=∠2,∠3=∠4,求证:AC∥DF,BC∥EF.证明过程如下:
∵∠1=∠2(已知),
∴AC∥DF(A.同位角相等,两直线平行),
∴∠3=∠5(B.内错角相等,两直线平行).
又∵∠3=∠4(已知)
∴∠5=∠4(C.等量代换),
∴BC∥EF(D.内错角相等,两直线平行).
上述过程中判定依据错误的是( )
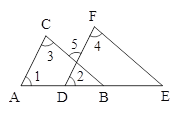
A. A B. B C. C D. D
科目:初中数学 来源: 题型:
【题目】为了能以“更新、更绿、更洁、更宁”的城市形象迎接2011年大运会的召开,深圳市全面实施市容市貌环境提升行动.某工程队承担了一段长为1500米的道路绿化工程,施工时有两张绿化方案: 甲方案是绿化1米的道路需要A型花2枝和B型花3枝,成本是22元;
乙方案是绿化1米的道路需要A型花1枝和B型花5枝,成本是25元.
现要求按照乙方案绿化道路的总长度不能少于按甲方案绿化道路的总长度的2倍.
(1)求A型花和B型花每枝的成本分别是多少元?
(2)求当按甲方案绿化的道路总长度为多少米时,所需工程的总成本最少?总成本最少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中∠C=90°,∠A=30°,BC=2,点P,Q,R分别是AB,AC,BC上的动点,PQ+PR+QR的最小值是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若BM+CN=9,则线段MN的长为( ) 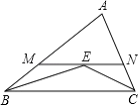
A.6
B.7
C.8
D.9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,对正方形纸片ABCD进行如下操作: 
(i)过点D任作一条直线与BC边相交于点E1(如图①),记∠CDE1=α1;
(ii)作∠ADE1的平分线交AB边于点E2(如图②),记∠ADE2=α2;
(iii)作∠CDE2的平分线交BC边于点E3(如图③),记∠CDE3=α3;
按此作法从操作(2)起重复以上步骤,得到α1 , α2 , …,αn , …,现有如下结论:①当α1=10°时,α2=40°;②2α4+α3=90°; ③当α5=30°时,△CDE9≌△ADE10;④当α1=45°时,BE2= ![]() .
.
其中正确的个数为( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,△ABC的三个顶点坐标分别为A(1,1),B(4,0),C(4,4).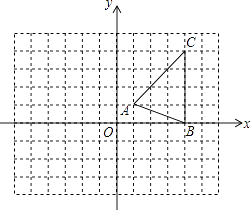
(1)按下列要求作图:
①将△ABC向左平移4个单位,得到△A1B1C1;
②将△A1B1C1绕点B1逆时针旋转90°,得到△A2B2C2 .
(2)求点C1在旋转过程中所经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=90°,AD⊥BC,垂足为D.
(1)求作∠ABC的平分线(要求:尺规作图,保留作图痕迹,不写作法);
(2)若∠ABC的平分线分别交AD,AC于P,Q两点,证明:AP=AQ.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,(1)∠BED与∠CBE是直线________,________被直线________所截形成的________角;
(2)∠A与∠CED是直线________,________被直线________所截形成的________角;
(3)∠CBE与∠BEC是直线________,________被直线________所截形成的________角;
(4)∠AEB与∠CBE是直线________,________被直线________所截形成的________角.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某旅游景区上山的一条小路上,有一些断断续续的台阶.下图是其中的甲、乙两段台阶路的示意图.请你用所学过的有关统计知识(平均数、中位数、方差和极差)回答下列问题:
(1)两段台阶路有哪些相同点和不同点?
(2)哪段台阶路走起来更舒服?为什么?
(3)为方便游客行走,需要重新整修上山的小路.对于这两段台阶路,在台阶数不变的情况下,请你提出合理的整修建议.
图中的数字表示每一级台阶的高度(单位:cm),并且数据15,16,16,14,14,15的方差s甲2=![]() ,数据11,15,18,17,10,19的方差s乙2=
,数据11,15,18,17,10,19的方差s乙2=![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com